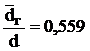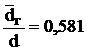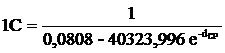СОРТОВОЙ
СОСТАВ КРУГЛЫХ ЛЕСОМАТЕРИАЛОВ И
ВЫХОД ПИЛОМАТЕРИАЛОВ И
ЗАГОТОВОК ОБЩЕГО НАЗНАЧЕНИЯ
Чамеев В.В., Гаева Е.В., Харисов П.Е. (УГЛТУ, г. Екатеринбург,
РФ)
HIGH-QUALITY
STRUCTURE of ROUND FOREST PRODUCTS And OUTPUT of SAW-TIMBERS And
PREPARATIONS of the GENERAL PURPOSE
При проектировании технологических процессов лесообрабатывающих цехов
лесопромышленных предприятий нужны сведения по сортовому составу сырья и выходу
готовой продукции из него. Для определения посортного
выхода пиломатериалов в ЦНИИМОД разработаны Руководящие техникоэкономические
материалы по нормированию расхода сырья и материалов в производстве
пиломатериалов (
Применительно к круглым лесоматериалам из сосны их сортность определяется в двух вариантах: а – в кп «СЫРЬЁ» по ГОСТ 9463-88 на основе математических моделей сырья и ограничений на пороки, приведённые в ГОСТ 9463-88; б – в кп «ПРОДУКЦИЯ» по ГОСТ 9463-72 на базе тех же математических моделей сырья, но с учётом ограничений на пороки по ГОСТ 9462-72. Такой подход позволяет применять в расчётах нормативы ЦНИИМОД посортных выходов пиломатериалов.
Основными сортообразующими пороками в
математической модели сырья приняты гниль, сучки и кривизна. I-й сортообразующий порок в математической модели представлен
случайной величиной Х с типом вероятностного распределения Pх, средним
значением 
, средним квадратическим
отклонением (СКО) σх, вероятностью
его появления Рп с указанием зависимостей Pх,
, σх, и Рп от доминирующих факторов.
Ниже представлена математическая модель сортообразующих пороков для сосновых бревен. Параметры модели cоответствуют сырью лесопромышленных предприятий Уральского региона. Для составления математической модели были использованы литературные источники и данные кафедры ТиОЛП УГЛТУ. Основные параметры модели сведены в таблице 1.
Наличие гнили в
бревнах характеризуется следующими параметрами: встречаемость бревен с гнилью РГ,
в т.ч. со сквозной РГС (вероятность встречи бревна с гнилью с
выходом на один торец РГО = РГ - РГС), степень
поражения гнилью торцов бревен в долях их толщины dг/d (среднее значение 
г/d, стандарт σdг/d, закон вероятностного
теоретического распределения), протяженностью напённой и стволовой гнили (среднее 
ГН и ГС, СКО 
и 
).
Встречаемость бревен с гнилью PГ и PГС возрастает с увеличением di,
что не противоречит биологическим свойствам древесины к загниванию. Уравнения
зависимостей г/d=ƒ(di)
и σdг/d=ƒ(di) следует считать
приближенным из-за недостаточного объёма исходного статистического материала.
Для практических целей использованы значения г/d и σdг/d для сырья из средней группы по толщине
(di
≤ г/d не противоречит
нормальному распределению. Некоторые выборки, с худшей сходимостью,
одновременно описываются и законом Эрланга.
Таблица
1 – Содержание сосновых брёвен с
пороками и их размерная характеристика
|
Регрессионные
уравнения |
Коэффициенты
уравнений определены
при |
|
|
14 ≤ di≤
|
|
|
15 ≤ di≤
|
|
|
di
≤ |
|
|
di
≤ |
|
σdг/d = 0,196 |
di
≤ |
|
σdг/d = 0,228 |
di
≤ |
|
|
dгн ≤ |
|
|
0,18 < dгн < |
|
|
0,6 ≤ dгн
≤ |
|
|
12 ≤ di
≤ |
|
|
12 ≤ di
≤ |
|
|
12 ≤ di
≤ |
|
|
di
≤ |
|
|
di
≥ |
; 
; 
; 
Протяженность напённой гнили в сосновых брёвнах зависит от степени пораженности ею торца. Чем сильнее развита напённая гниль, тем выше она поднимается по стволу. По геометрической форме центральные гнили округлого сечения наиболее близки к параболоиду с образующей в виде параболы. Для бревен комлевой вырезки длина напённой гнили зависит от диаметра гнили на торце бревен dГ. Для брёвен из вершинной и срединной частей хлыстов распределение длины стволовой гнили ℓГС установить невозможно. Для дальнейших расчётов принимается по равномерному закону.
Для бревен из вершинной и срединной части хлыстов распределение длины стволовой гнили ℓГС установить невозможно.
Характеристика сучков в круглых
лесоматериалах включает статистические описания: встречаемость бревен с сучками
РС, число сучков на единицу длины бревна nC1
и толщину сучков dС. Доля бревен с сучками уменьшается с
увеличением di и существует
статистическая связь РС =
ƒ(di). Число сучков на 
и СКО σn,
для разных групп сырья по толщине позволяет в модели принять их независимыми от
ступеней толщины сырья. Принятые значения и σn, приведены в табл. 1. Средняя толщина сучка С и стандарт σdc находятся в
статистической зависимости от di. Эмпирические
распределения сучков по толщине не противоречат логарифмическому
нормальному
Кривизна К,
как случайная величина, подчиняется вероятностному закону со средним значением 
и стандартом σК, характеризуется встречаемостью брёвен с
кривизной РК. У сосны сравнительно небольшое число бревен с
кривизной. С увеличением di значение РК снижается.
Эмпирические распределения кривизны К асимметричны и
одинаково хорошо описываются как логнормальным законом,
так и законом Эрланга. Связь статистик и σК с толщиной сырья di
очень проблематична. Для практического пользования принимается модель кривизны,
приведенная в табл. 1.
Реализация приведённой
математической модели на ЭВМ в кп «СЫРЬЁ» позволила
получить сортовой состав круглых лесоматериалов из сосны по ГОСТ 9463-88 для
выработки пиломатериалов и заготовок общего назначения по ГОСТ 8686-86. При имитационном
моделировании потока брёвен для рамной распиловки со средней длиной
, %.
Соответственно брёвна 2-го и 3-го сортов, %
;
.
Анализ приведённых уравнений
регрессий показывает, что с увеличением средней толщины сырья на
Для определения выхода готовой продукции из сырья используются данные сортового состава сырья по ГОСТ 9463-72, полученные по кп «ПРОДУКЦИЯ», %
; 
;
;
.
Сопоставление полученных результатов моделирования сортового состава сырья со сведениями, имеющимся в различных источниках позволяют сделать вывод, что математические модели параметров сырья адекватны.
Достижение адекватности математических моделей параметров сырья позволяет, используя нормативы посортных выходов пиломатериалов заложенных в кп «ПРОДУКЦИЯ», определить по ней выход готовой продукции в зависимости от способа раскроя круглых лесоматериалов несортированного и сортированного на размерные группы сырья.
Результаты исследований приведены в
таблице 2. При распиловке сырья с брусовкой выход
пиломатериалов повышенной сортности (1 и 2 с) с увеличением среднего диаметра
пиловочных брёвен с 16 до
Результаты по сортовому составу сырья и выходу готовой продукции из него можно использовать технологам по лесопилению в технологических расчётах, а также при имитационном моделировании технологического процесса лесообрабатывающего цеха по кп «ПОТОК» комплекс-программы «ЦЕХ» в виде входной информации.
Таблица 2 – Посортный выход сосновых пиломатериалов (ГОСТ 8486-86) для условий Урала при распиловке пиловочного сырья (ГОСТ 9463-88)
|
Регрессионные уравнения |
Коэффициенты уравнений определены при пилении: |
№ уравнений |
|
с брусовкой из несортированного сырья на обрезные пиломатериалы |
||
|
|
dcp = 16 … 30 cм |
1 |
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
с брусовкой при
различных отклонениях диаметра сырья |
||
|
|
|
6 |
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
||
|
Продолжение табл. 2 |
||
|
с брусовкой из
сортировочно-размерных групп сырья |
||
|
|
dcp = 14 … |
11 |
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
вразвал из несортированного сырья на необрезные пиломатериалы |
||
|
|
dcp = 16 … |
16 |
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
вразвал из 4-х размерно-сортировочных
групп сырья с дробностью сортировки |
||
|
|
|
21 |
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
