Моделирование
процесса окорки лесоматериалов на основе
теории нечетких множеств
Побединский В.В., Берстенёв
А.В., Шуняев С.Н.
(УГЛТУ, г. Екатеринбург, РФ) nto@krovtreade.ru
Одним из наиболее эффективных путей совершенствования роторных окорочных станков (РОС) является использование системы автоматического управления (САУ) гидроприводом механизма прижима режущего инструмента (РИ). При этом возникает ряд исследовательских задач, которые ранее не рассматривались. В ходе прогресса развитие элементной базы гидропривода и микропроцессорной техники позволило решить первоочередную задачу - разработку структурной схемы САУ РИ [1], на основе которой создается в дальнейшем конструктивное решение. Для этих целей схемная реализация САУ предусматривает синтез параметров системы с помощью передаточной функции и использования спектральных характеристик динамических воздействий на механизм резания со стороны микропрофиля поверхности обрабатываемого лесоматериала.
Получить такие данные экспериментально чрезвычайно сложно, а тем более для всего породного и сортиментного состава будет практически невозможно, поэтому единственным выходом в этой ситуации является использование метода математического моделирования.
При обработке лесоматериалов динамические нагрузки, действующие на режущий механизм, обусловливаются пороками древесины (кривизна, сучки, овальность и т. д.). Для исследования САУ РИ и оценки некоторых параметров динамических нагрузок необходима автокорреляционная функция, описывающая микропрофиль поверхности древесины.
Процесс обработки лесоматериала в РОС складывается из двух движений:
- главного движения - вращательного движения ротора с инструментами вокруг бревна;
- вспомогательного движения подачи - поступательного, вдоль оси лесоматериала.
Данные о статистических характеристиках микропрофиля поверхности вдоль указанных направлений имеются, и поверхность лесоматериала описывается вероятностными методами. Однако в процессе обработки инструмент движется по винтовой линии на поверхности лесоматериала, наклон которой зависит от скорости вращения ротора, скорости подачи и диаметра бревна. Определить микропрофиль строго той поверхности, по которой движется инструмент, в этом случае не представляется возможным.
Такой процесс описан имитационной моделью [2], которая позволяет статистически оценить поверхность лесоматериала, но установить функциональную зависимость динамических нагрузок от влияния различных микронеровностей, и тем более их совместного действия, чрезвычайно сложно. Поэтому необходимые для проектирования станков данные определяются на основании экспериментальных исследований [3], но и в этом случае получают только некоторые параметры процесса динамических нагрузок, а функциональные зависимости между характеристиками древесины, режимами и случайным процессом нагрузок не определяются. Основная причина здесь в том, что имеется большое количество неопределенностей, при которых имитационное моделирование будет недостаточно обосновано.
В начале развития ЭВМ появилось целое направление в моделировании. Были разработаны соответствующие алгоритмы, методы, теоретические подход, но их внедрение ограничивалось возможностями первых ЭВМ. В настоящее время произошел качественный прорыв в развитии информационных технологий, что потребовало развития теоретической области и разработки, соответственно, адекватных подходов к созданию математического обеспечения в прикладных отраслях науки и техники.
Одним из таких направлений, которое с момента возникновения получает все более широкое применение, является математический аппарат теории нечетких множеств (ТНМ).
В области моделирования с использованием нечеткой логики связан новый этап развития. Так, начиная с 60-70 годов имитационное моделирование, игровые методы позволяли решать многие задачи для объектов с вероятностными параметрами или условий неопределенности. Но при этом ограничивалась подробность описания объектов, чтобы при невысоких ресурсах вычислительной техники обеспечить достаточный уровень точности. Прогресс в этой области привел к тому, что в настоящее время уровень детализации часто ограничивается не параметрами компьютера или математического аппарата, а возможностями разработчика.
Нечеткое моделирование оказывается особенно эффективным, когда процессы являются слишком сложными для анализа с помощью общепринятых количественных методов, или когда исходные данные интерпретируются неточно или неопределенно.
Практикой доказано, что во многих случаях нечеткое моделирование позволяет более адекватно описывать объекты с неопределенностью и дает лучшие результаты, чем получаемые на основе детерминированных или вероятностно-статистических моделей [4,5,6].
ТНМ применяется для описания значений, которые принимает лингвистическая переменная на основе нечетких высказываний, где функция принадлежности элемента множеству не бинарна (да/нет), а может принимать любое значение в диапазоне от ноля до единицы. Это дает возможность формализовать понятия, нечеткие по самой своей природе "хороший", "высокий", "слабый" и т.д. и выполнять над такими величинами весь спектр логических операций - объединение, пересечение, отрицание и др.
Одним из важнейших достоинств ТНМ является возможность использования нечетких множеств (НМ) при моделировании задач, в которых отсутствует полная информация о рассматриваемой системе. При этом НМ рассматриваются как вероятностные распределения и ТНМ должна использоваться с теорией вероятности. При таком совместном использовании различных по сути методов исследования и достигаются наиболее достоверные результаты [4,5].
В данном случае, когда оценка параметров объекта, развитие процесса носит неопределенный характер, наиболее правильным будет использование концепции нечеткого моделирования системы.
Рассмотрим с точки зрения ТНМ исследуемый процесс.
Для оценки динамических параметров действующих на механизм резания служит ключевое событие в процессе обработки – встреча лезвия короснимателя с неровностью на поверхности лесоматериала (сучки, пороки древесины). Значение ударной нагрузки можно интерпретировать как лингвистическую переменную. Область определения переменной на практике определяется экспериментальным путем.
На вход модели поступают данные, соответствующие характеристикам реального процесса. Система нечеткого вывода предназначена для преобразования входных данных в выходные на основе использования правил нечеткой продукции (ПНП), поэтому содержит базу ПНП, предназначенную для нечеткого вывода на основе неких правил. Такие правила представлены в форме лингвистических высказываний (ЛВ), которые реализованы на основе нечетких условий или высказываний.
Процесс нечеткого вывода включает следующие этапы:
1 Формирование базы правил системы нечеткого вывода;
2 Фаззификация входных данных;
3 Формирование аппарата нечетких рассуждений;
3.1 Агрегирование подусловий в нечетких правилах;
3.2 Активизация или композиция подзаключений в ПНП;
3.3 Аккумулирование заключений нечетких правил продукций;
4 Дефаззификация выходных данных.
С позиций ТНМ в этой ситуации мы имеем «чёткие» данные о каждой отдельной характеристике - в продольном направлении и по окружности бревна. Простое математическое сложение характеристик микропрофиля вдоль и по окружности не будет соответствовать микропрофилю поверхности по винтовой линии. Если теперь на основании характеристик микропрофиля в известных направлениях построить лингвистические высказывания, то с помощью аппарата ТНМ можно получить «чёткий» вывод картины динамических нагрузок в рамках решения задачи нечёткого вывода. Точность решения задачи НВ достигается посредством увеличения числа различных вариантов лингвистических высказываний (базы правил).
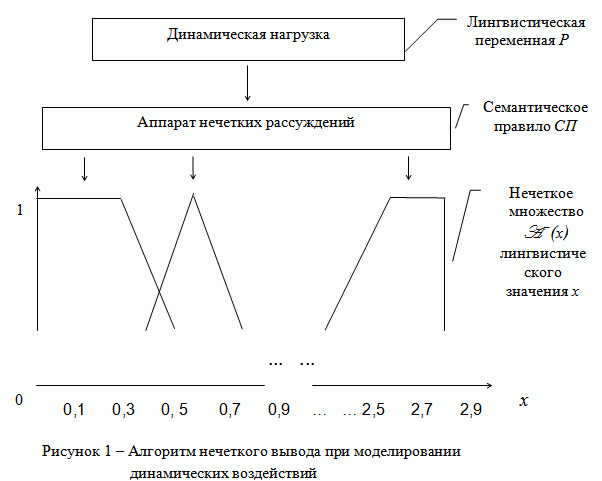
Графическая интерпретация модели возникновения динамических нагрузок на основе нечетких множеств показана на рисунке 1.
На схеме динамические воздействия на РИ представляют лингвистическую переменную Р , которая определяется следующими параметрами:
Р = [Х, х, A , С, СП],
где Х - область определения переменной (универсум);
х - значение переменной;
A - нечеткое множество на области определения Х;
С - синтаксическое правило для определения лингвистического
значения нечеткого множества A ;
СП - семантическое правило для связи лингвистического
значения множества с соответствующим множеством A .
На нижнем графике изображена градация для синтаксического правила С определения лингвистического значения нечеткого множества A . Значение функции принадлежности нечеткому множеству A задается в интервале [0,1].
Базу правил составляет система нечетких высказываний различного вида, например:
- «Если макронеровность бревна БОЛЬШАЯ, а высота сучка МАЛЕНЬКАЯ,
то динамическая нагрузка СРЕДНЯЯ»;
- «Если макронеровность бревна БОЛЬШАЯ, а высота сучка СРЕДНЯЯ,
то динамическая нагрузка БОЛЬШАЯ»;
- «Если макронеровность бревна БОЛЬШАЯ, и высота сучка БОЛЬШАЯ,
то динамическая нагрузка ОЧЕНЬ БОЛЬШАЯ».
Количественные значения параметров принимаются на основе ряда экспериментальных исследований.
В рассматриваемой задаче для детального учета особенностей процесса таких высказываний построено значительно больше, и точность результатов достигается увеличением количества высказываний, описывающих процесс с различных позиций. С увеличением точности ЛВ, нечеткая логика приходит к стандартной, Булевой, что является подтверждением правильности подхода и адекватности разработанной модели.
На этапе фаззификации выполняется приведение известных количественных выражений или высказываний экспертов выраженных на естественном языке к нечеткому виду. Например, если пороки лесоматериала вызывающие динамические нагрузки распределяются следующим образом:
- количество сучков высотой
от 1 до
- количество сучков высотой
до
- количество сучков выше
Дальнейшие процедуры формализации направлены на получение так называемых нечетких множеств, определяющих его параметры.
Базовую архитектуру семантического правила составляют компоненты теории - агрегирование, активизация, аккумулирование, дефаззификация.
Из системы нечетких высказываний формируется база правил нечетких продукций. Далее, для получения нечеткого вывода выполняется этапы агрегирования и активизации. Первое представляет определение по каждому правилу степени истинности условий, а второе степень истинности подзаключений.
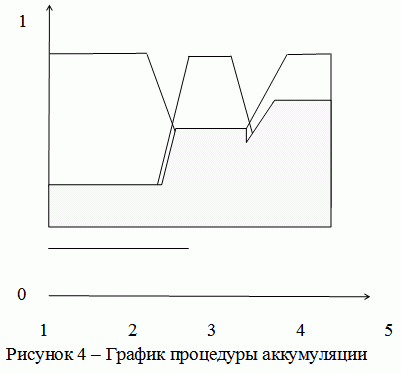
Для нахождения функции принадлежности выходной лингвистической переменной из всех степеней истинности подзаключений применяется процедура аккумулирования (объединения).
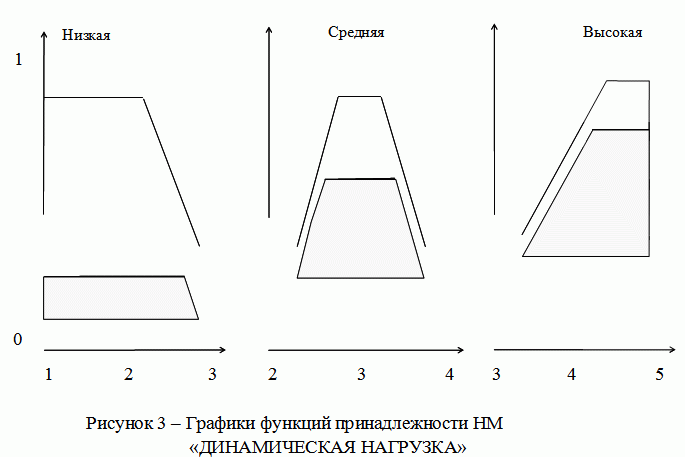
Перед процедурой аккумулирования предполагаются известными значения истинности всех подзаключений для каждого из правил базы правил системы нечеткого вывода в форме совокупности. Например, для лингвистической переменной «динамическая нагрузка» определены нечеткие множества A {НИЗКая}, B {СРЕДНЯЯ}, C {ВЫСОКАЯ} (рисунок 3). Результатом аккумуляции (рисунок 4) выходной лингвистической переменной будет логическое объединение, т.е.
|
|
|
|
нечеткое множество D = A υ B υ C ( знак “υ” является синонимом “v” логической операции ИЛИ).
Для случайных воздействий (распределения пороков на поверхности лесоматериала) используется метод имитационного моделирования, если для них имеются вероятностные параметры. В противном случае такие воздействия описываются введением нечеткости.
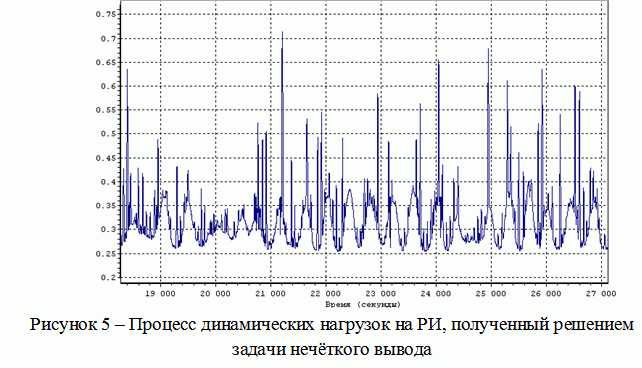
Разработанный на основе ТНМ алгоритм реализован в среде Delphi, где выполняется имитационное моделирование параметров лесоматериала, для организации нечеткого вывода в виде нейролингвистической сети ядро программы интегрировано с пакетом MatLab, в котором предусмотрены стандартные средства работы с НМ. Сопоставление амплитудных и спектральных характеристик динамических нагрузок, полученных при моделировании (рисунок 5) с результатами натурных экспериментов [3], показали достаточную адекватность математической модели реальному процессу окорки лесоматериалов.
Заключение
1 Применение теории нечетких множеств открывает новые возможности в совершенствовании конструкций режущего инструмента РОС с возможностью исследования систем автоматического управления.
2 Для наиболее достоверного математического описания процесса динамических нагрузок на режущий инструмент при обработке лесоматериалов следует совместно использовать вероятностные методы и теорию нечетких множеств.
3 При совместном использовании различных методов будет рациональнее организация структуры в среде объектно-ориентированного языка, например, Delphi, а для вычислений процедур нечеткого вывода обеспечить связь с приложением пакета MatLab. Реализация предложенного алгоритма в среде Delphi интегрированного с пакетом MatLab в виде нейролингвистической сети позволяет достаточно адекватно описать процесс динамических нагрузок в конструкции.
|
|
|
|
|
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1 Берстенёв А.В., Побединский
В.В., Санников С.П. Система автоматического управления рабочими органами
роторного окорочного станка. – Сборник докладов второй научно-техн.
конф. молодых специалистов. – Екатеринбург: УГЛТУ, 19 апреля
2 Побединский В.В. и др. Имитационная модель процесса окорки
лесоматериалов на роторных окорочных станках. – В кн.: Вклад ученых и
специалистов в развитие химико-лесного комплекса. / Тез. докл.
к Обл. научно-техн. конф. – Свердловск, УЛТИ, 1-3 февраля
3 Побединский В.В. и др. Методика экспериментальных исследований роторных
окорочных станков в производственных условиях. – В кн.: Вклад ученых и
специалистов в развитие химико-лесного
комплекса. / Тез. докл. к Обл.
научно-техн. конф. –
Свердловск, УЛТИ, 1-3 февраля
4 Юфин
С.А., Семенюк-Ситников В.В. Применение нечетких
экспертных систем в геотехническом строительстве. «Строительные материалы,
оборудование и технологии XXI
века», №1,2,
5 Берстенев
А.В., Побединский В.В., Шуняев С.Н. Применение алгоритмов
нечеткого вывода в моделировании объектов с нестрого определенными параметрами.
– В кн.: Ракетно-космическая техника. Научно-техн. сб. Системы управления ракетных комплексов. III науч.-техн.конф. молодых специалистов НПОА: -Екатеринбург:
Федер.аг. ФГУП
НПО «Автоматика» им. Академика Н.А.Семихатова, 9-11 апреля
6 Бекузаров И., Дедегкаев А.Г Нечётко-логические модели и алгоритмы. – Владикавказ: Северо-Кавказский государственный технологический университет, Факультет электронной техники, кафедра промышленной электроники. 2001г.