Объем   сбеговой   зоны   бревен

Уласовец  В. Г.  (УГЛТУ, г. Екатеринбург, РФ)  mod@usfea.ru

Volume   of   a   side   zone   of   logs

В соответствии с данными лесной таксации при большом разнообразии образующих поверхности стволов деревьев основной объем пиловочных бревен имеет форму, близкую к усеченному параболоиду или усеченному конусу [1, 2]. При этом общий объем любого бревна V, можно выразить формулой

V = V_ц + V_сб,                                                         (1)

где  V_ц   - объем цилиндрической  части  бревна,  который  принято  называть цилиндрической кубатурой бревна, равный

,                                                       (2)    

 где    d  - диаметр бревна в вершине; 

          L  -  длина  бревна.

V_сб  -  объем сбеговой зоны бревна.

При форме ствола приравненной к усеченному параболоиду вращения объем бревна вычисляют по формуле

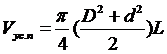,                                               (3)

где  D   - диаметр  бревна в комле; 

При форме ствола приравненной к усеченному конусу объем бревна вычисляют по формуле                

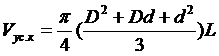.                                        (4)

С учетом того, что D = dK формулы  (3  и  4) будут выглядеть следующим образом:

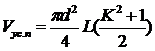,                                              (5)

.                                            (6)

Из выражений 5 и 6 видно, что исследуемый объем зависит от величины вершинного диаметра бревна, его длины и коэффициента сбега  К.

С увеличением коэффициента сбега происходит увеличение объема бревна за счет увеличения сбеговой зоны V_сб, величину которой можно рассчитать по следующей формуле:

 - для  усеченного  параболоида                                              

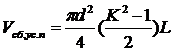,                                             (7)

при  этом объем зоны сбега от объема всего бревна составит,  %,         

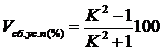;                                             (8)

а объем цилиндрической кубатуры от объема всего бревна  составит,  % 

.                                                (9)

     - для усеченного конуса величину сбеговой зоны V_сб можно рассчитать по следующей формуле:

,                                  (10)

при  этом объем зоны сбега от объема всего бревна составит,  %,         

,                                     (11) 

а объем цилиндрической кубатуры от объема всего бревна составит, %

.                                            (12)

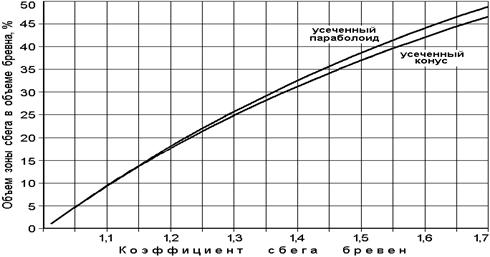
На графике (рисунке 1), построенном по формулам (8) и (11), показано изменение (в %) объема сбеговой зоны в объеме бревна в зависимости от формы образующей бревна и его коэффициента сбега.

     Из графика (рис. 1) видно, что для всех значений коэффициентов сбега объем сбеговой зоны в бревнах, форма которых приравнена к усеченному параболоиду, больше, чем у имеющих форму усеченного конуса, причем с увеличением коэффициента сбега от К = 1,05 до К = 1,7 объем сбеговой зоны бревен, приравненных к усеченному параболоиду, изменяется от 4,87%  до 48,6%, а в бревнах, приравненных к усеченному конусу, – от 4,84%  до  46,3%.

         Из приведенных выше данных (рисунок 1) видно, что объем сбеговой зоны бревен с любой боковой образующей значителен, поэтому разработка теоретических решений по ее рациональному раскрою представляется важнейшей технической и экономической задачей лесопиления.

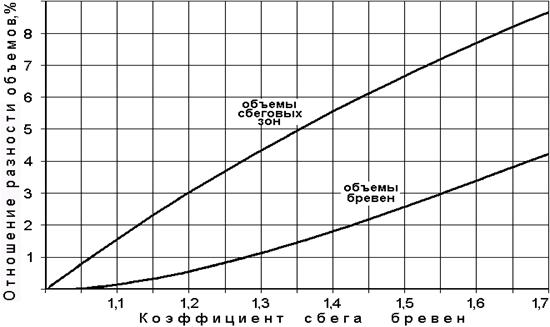
     Относительные изменения объемов сбеговых зон и объемов бревен в зависимости от их формы и величины коэффициентов сбега представлены на графике (рисунок 2). На верхней кривой графика (рисунок 2) показана величина отношения (в %) разности объемов сбеговых зон бревен, имеющих форму усеченного параболоида и усеченного конуса, к объему сбеговой зоны бревна, имеющего вид усеченного параболоида.

Рисунок 1 –  Изменение объема сбеговой  зоны  бревна

При изменении коэффициентов сбега от К = 1,05 до  К = 1,7 относительная  разность  объемов  сбеговых  зон  бревен  изменяется соответственно от 0,8 до  8,6%.  Нижняя кривая на этом графике изображает величину отношения (в %) разности объемов бревен формы усеченный параболоид и усеченный конус к объему бревна формы усеченный параболоид.

Рисунок 2 – Изменение  объемов  сбеговых  зон  и  объемов  бревен

в  зависимости  от  их  формы  и  величины  коэффициентов  сбега

При  изменении  коэффициентов сбега от К = 1,05 до К = 1,7 исследуемая относительная разность объемов бревен увеличивается соответственно от 0,04 до  4,2%.    

     Отмеченные выше закономерности изменения объемов бревен и их сбеговых зон, связанны с различной формой образующих, которую необходимо учитывать при теоретических исследованиях, связанных с поиском рациональных схем и способов раскроя пиловочника на пилопродукцию.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.  Анучин  Н.П. Лесная таксация /Н.П. Анучин. - М.: Лесн. пром-сть, 1982.        - 530 с.

2. Аксенов П.П. Теоретические основы  раскроя пиловочного сырья / П.П. Аксенов - М.: - Л.:  Гослесбумиздат, 1960. - 216 с.