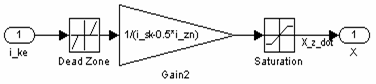Синтез математической модели
гидропривода механизма
резания роторного окорочного станка в
системе Matlab
Берстенев А.В., Побединский В.В.
(УГЛТУ, г.Екатеринбург, РФ) nto@krovtrade.ru
Synthesis of
mathematical model of a
hydrodrive of the
mechanism of cutting
the rotary debarking machine in
Matlab environment
Разработка сложной системы гидропривода короснимателя роторного окорочного станка требует на начальном этапе проведения математического моделирования для определения основных параметров системы. Подробное описание математической модели гидропривода механизма резания окорочного станка приведено в статье[1] [1] и отчёте [2].
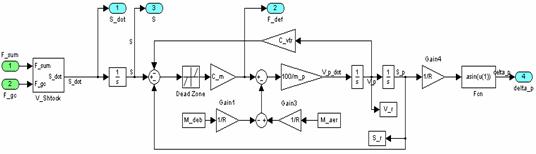
В соответствии с требуемыми параметрами гидропривода короснимателя (ГПК) и математической моделью была разработана математическая модель ГПК (рисунок 1,2) в подсистеме моделирования динамических процессов Simulink среды визуального моделирования MatLab.
|
|
|
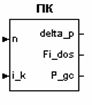
Рисунок 1- Блок ГПК |
На вход модели поступает значение перегрузки n и командный ток ![]() . На выходе формируется угол поворота устройства управления
(УО) относительно нулевого положения delta_p, угол
поворота вала датчика обратной связи Fi_dos и
значение силового усилия, оказываемое током гидроцилиндра P_gc.
. На выходе формируется угол поворота устройства управления
(УО) относительно нулевого положения delta_p, угол
поворота вала датчика обратной связи Fi_dos и
значение силового усилия, оказываемое током гидроцилиндра P_gc.
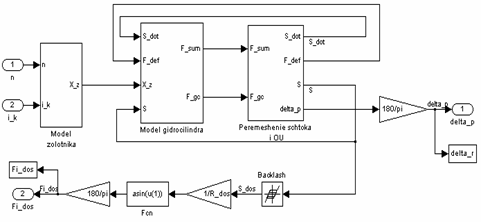
Модель гидропривода короснимателя состоит из следующих подсистем:
- «Модель золотника»;
- «Модель гидроцилиндра»;
- «Модель процесса перемещение штока и УО»;
- «Датчик обратной связи (ДОС)».
Подсистема «Модель золотника» формирует
относительное перемещение золотника ЭГУ ![]() . Структура подсистемы представлено на рисунке 3.
. Структура подсистемы представлено на рисунке 3.
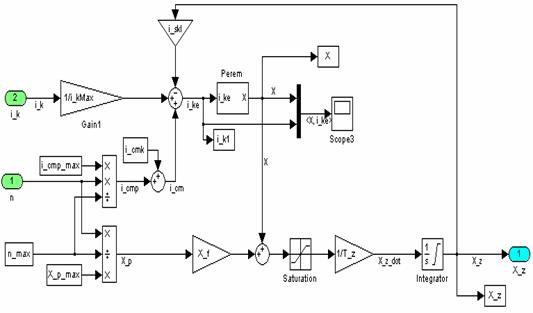
В данной подсистеме реализуются уравнения (23-30) математической модели ПК. На вход поступает командный ток i_k и значение перегрузки n. В зависимости от полярности командного тока струйная трубка отклоняется вправо (при положительном токе) или влево (при отрицательном токе).
|
|
|
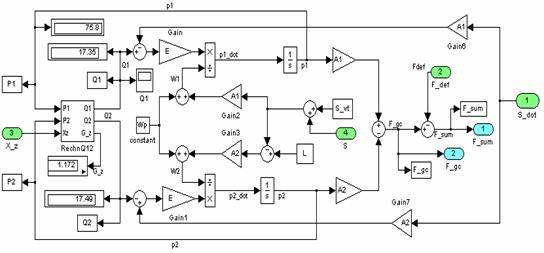
Рисунок 2 – Структурная схема блока ГПК |
|
|
|
Рисунок 3 – Структурная схема подсистемы "Модель золотника" |
Коэффициент 1/i_kMax служит для перевода тока i_k в
относительный командный ток. Эквивалентный командный ток i_ke поступает на вход блока «Перемещение
струйной трубки», структура которой представлена на рисунке 4. В этом блоке
реализуются уравнения (24) и (25) математической модели ПК. Причём коэффициент
К в уравнении (25) должен быть равен 1, иначе зависимость ![]() имеет разрыв. Блоком «Dead Zone» представлена зона
нечувствительности по току шириной i_zn
(левая граница – 0.5 · i_zn, правая граница 0.5 · i_zn).
Блок «Saturation»
реализует ограничение перемещения
имеет разрыв. Блоком «Dead Zone» представлена зона
нечувствительности по току шириной i_zn
(левая граница – 0.5 · i_zn, правая граница 0.5 · i_zn).
Блок «Saturation»
реализует ограничение перемещения ![]() значениями -1 и +1.
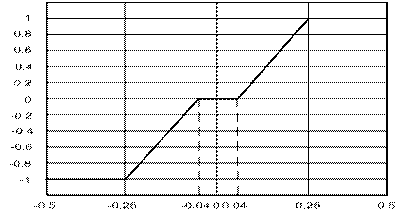
Зависимость относительного перемещения струйной трубки
значениями -1 и +1.
Зависимость относительного перемещения струйной трубки ![]() от эквивалентного
командного тока i_ke представлена на рисунке 5.
от эквивалентного
командного тока i_ke представлена на рисунке 5.
|
|
|
Рисунок 4- Структурная схема блока перемещение струйной трубки |
|
|
|
Рисунок 5 - Зависимость |
Полученное относительное перемещение ![]() подаётся на вход звена
расчёта скорости перемещения золотника (рисунок 3), которое вычисляет скорость
относительного перемещения золотника
подаётся на вход звена
расчёта скорости перемещения золотника (рисунок 3), которое вычисляет скорость
относительного перемещения золотника ![]() в зависимости от
относительного перемещения струйной трубки
в зависимости от
относительного перемещения струйной трубки ![]() . Блок «Saturation»
реализует ограничение перемещения
. Блок «Saturation»
реализует ограничение перемещения ![]() значениями минус 1 и
+1. В блоке «Gain»
константа T_z = 0.0025. Путём
интегрирования
значениями минус 1 и
+1. В блоке «Gain»
константа T_z = 0.0025. Путём
интегрирования ![]() вычисляется
относительное перемещение золотника
вычисляется
относительное перемещение золотника ![]() .
.
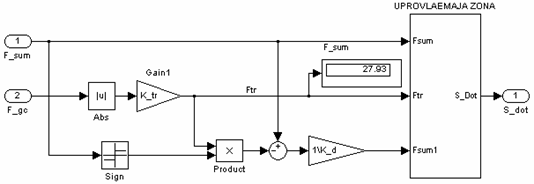
Подсистема «Модель гидроцилиндра» формирует силы, действующие на шток гидроцилиндра Fгц и Fсум. Структура этой подсистемы представлена на рисунке 6.
|
|
|
Рисунок 6- Структурная схема подсистемы "Модель гидроцилиндра" |
В данной подсистеме реализуются уравнения (11)-(22) математической
модели ПК. На вход поступает относительное перемещение золотника ![]() . В зависимости от его значения золотник смещается вправо
(при отрицательном
. В зависимости от его значения золотник смещается вправо
(при отрицательном ![]() ) или влево (при положительном
) или влево (при положительном ![]() ). Соответственно открывается один из каналов, по которым под
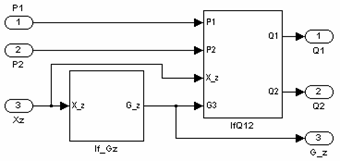
давлением движется рабочая жидкость, поступающая в полость ГЦ. Расход рабочей
жидкости вычисляется с помощью блока «Расход рабочей жидкости» (рисунок 7).
). Соответственно открывается один из каналов, по которым под
давлением движется рабочая жидкость, поступающая в полость ГЦ. Расход рабочей
жидкости вычисляется с помощью блока «Расход рабочей жидкости» (рисунок 7).
|
|
|
Рисунок 7- Структурная схема блока "Расход рабочей жидкости" |
На вход блока поступает относительное
перемещение золотника ![]() и давление Р1
и Р2 (из обратной связи). В зависимости от значения
и давление Р1
и Р2 (из обратной связи). В зависимости от значения ![]() из выражения (21),
(22) определяется суммарная проводимость рабочего окна и канала золотникового
распределителя Gz.
На основании давлений Р1,Р2, относительное перемещение
золотника
из выражения (21),
(22) определяется суммарная проводимость рабочего окна и канала золотникового
распределителя Gz.
На основании давлений Р1,Р2, относительное перемещение
золотника ![]() и проводимость Gz.в блоке «Расчёт
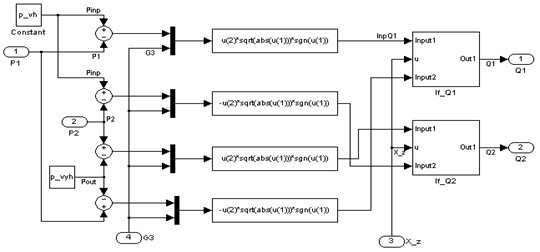
Q1, Q2» (рисунок 8)
вычисляются расходы рабочей жидкости Q1, Q2
по формулам (18), (19).
и проводимость Gz.в блоке «Расчёт
Q1, Q2» (рисунок 8)
вычисляются расходы рабочей жидкости Q1, Q2
по формулам (18), (19).
Полученные расходы Q1, Q2, а также объёмы бесштоковой и штоковой полостей ГЦ W1 и W2 в свою очередь позволяют рассчитать давления Р1 и Р2, определяющие силу Fгц, действующую на шток ГЦ. А сила Fсум – есть разница силы Fгц и силы деформации Fдеф.
|
|
|
Рисунок 8 – Структурная схема блока "Расчёт Q1, Q2". |
В подсистеме «Перемещение штока и УО» формируются скорость перемещения штока S_dot, перемещение штока S, сила деформации Fдеф и перемещение короснимателя delta_r. Структурная схема этой подсистемы представлена на рисунке 9.
|
|
|
Рисунок 9 – Структурная схема подсистемы "Перемещение штока и УО". |
В этой подсистеме реализуются уравнения (1) -
(10) математической модели ПК. На вход подсистемы поступают силы ![]() и
и ![]() . С помощью блока «Скорость перемещения штока» (рисунок 10)
рассчитывается по формуле (9) скорость перемещения штока, при этом учитывается,
что на механических упорах
. С помощью блока «Скорость перемещения штока» (рисунок 10)
рассчитывается по формуле (9) скорость перемещения штока, при этом учитывается,
что на механических упорах ![]() .
.
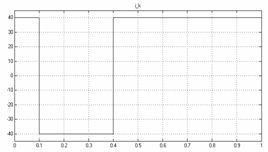
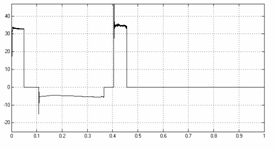
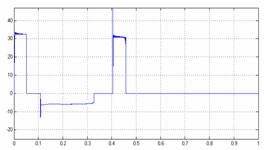
Для получения характеристик модели гидропривода механизма резания роторного окорочного станка в качестве задающего воздействия использовался командный ток, изменяющийся во времени скачками от 40 мА до минус 40мА.
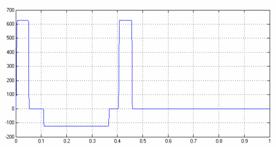
На рисунке 11 показаны командный ток управления, скорость выдвижения штока гидроцилиндра и угловая скорость вращения короснимателя вокруг оси закрепления. Графики в левой колонке – результат моделирования без внешней нагрузки.
Как видно из графиков, скорость выдвижения штока (участок времени 0 – 0,1 с) составляет 300м/с, угловая скорость короснимателя 573 град/с. Аналогично, скорость втягивания штока (участок времени 0,1 – 0,5 с) составляет 40м/с, угловая скорость короснимателя 102 град/с. В момент достижения штоком упора, его скорость принимает нулевое значение.
|
|
|
Рисунок 10- Структурная схема блока "Скорость перемещения штока". |
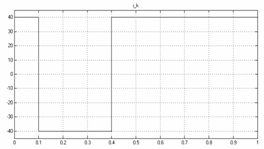
Графики в правой колонке демонстрируют результат моделирования с учётом нагрузки на коросниматель 2000 Н.
|
Моделирование без внешней нагрузки |
Моделирование с внешней нагрузкой |
|
Командный ток управления (мА). |
|
|
|
|
|
Скорость перемещения штока ГЦ (см/с). |
|
|
|
|
|
Угловая скорость вращения короснимателя (град/сек). |
|
|
|
|
|
Рисунок 11 - Моделирование процессов гидравлического привода без нагрузки и с нагрузкой до 2000 Н |
|
Из приведённых результатов моделирования следует, что скорость выдвижения штока ГЦ значительно больше, чем скорость втягивания. Такой эффект обусловлен конструктивной особенность моделируемого гидропривода. Причиной этого является неравномерность нагрузки на гидропривод при его движении в противоположные стороны. Так при опускании короснимателя, действие производится только за счёт усилия прижима гидропривода с учётом отрицательного вклада центробежной силы, действующей на управляемый элемент.
При поднятии короснимателя к усилию гидропривода с положительным знаком добавляются центробежная сила и динамическая нагрузка от действия обрабатываемой поверхности. Таким образом, для улучшения динамических характеристик усилие гидроцилиндра при втягивании снижено за счёт уменьшения эффективной площади сечения штоковой области ГЦ.
Заключение
Разработанная математическая модель гидропривода механизма резания роторного окорочного станка является составной часть модели системы управления режущими инструментами станка, в которую помимо рассмотренной системы входят модель САУ и модель процесса возмущений от воздействия обрабатываемой поверхности лесоматериала.
Реализация предложенной в [1] математической модели в среде моделирования динамических процессов MatLab позволяет учесть важнейшие особенности механизма, его физические параметры и использовать при проектировании системы управления рабочими органами роторного окорочного станка.
Использование при проектировании пакета MatLab обеспечивает наиболее рациональный подход к разработке, позволяет объединять составные части модели, производить её детальный анализ и отработку параметров конструкции.
Библиографический список
1. Берстенёв А.В., Побединский В.В., Санников С.П.
Система автоматического управления рабочими органами роторного окорочного
станка. – Сборник докладов второй научно-техн. конф. молодых специалистов. –
Екатеринбург: УГЛТУ, 19 апреля
2. Лаборатория динамических систем. Отчёт о доработке модели рулевого
привода. – Федеральное космическое агентство ГУП НПО «Автоматика» им. Академика
Н.А.Семихатова
3. Дорф Р.К., Бишоп Р. Х. Современные системы управления. – М.: «Лаборатория Базовых Знаний», 2004г.- 832с.
4. Лазарев Ю. Моделирование процессов и систем в MatLab. – Санкт-Петербург: «Питер», 2005г. - 512с.