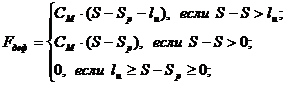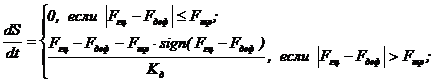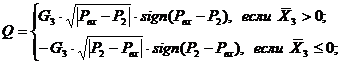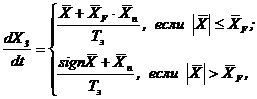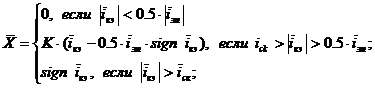Математическая  модель  гидропривода  рабочего  органа  роторного  окорочного  станка

Берстенев А.В., Побединский В.В.

(УГЛТУ, г.Екатеринбург, РФ)  nto@krovtrade.ru

Mathematical  model  of  a hydrodrive  of  working body  the  rotary  debarking  machine

 

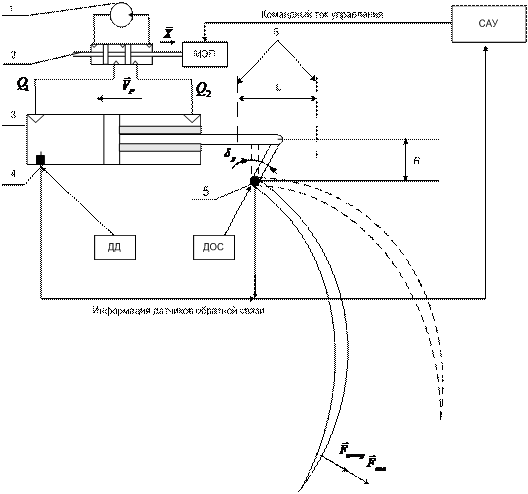
Структурная реализация конструктивного решения гидропривода режущего инструмента роторного окорочного станка [1] предусматривает использование механизма с системой автоматического управления (САУ) [2,3]. Для исследования работы такой конструкции (рисунок 1) необходима модель гидравлического привода. Ниже приводится описание разработанной математической модели гидропривода для станка       ОК-63.

 

1 – гидравлический насос; 2 – золотник; 3 – гидроцилиндр; 4 – датчик давления;

5 – круговой индукционный датчик обратной связи.

Рисунок 1  - Принципиальная схема гидравлического привода рабочего

органа окорочного станка.

 

Вращательное движение короснимателя (органа управления) для модели станка описывается следующими уравнениями:

Значение угла поворота dр  управляющего (УО) органа относительно исходного положения находится по формуле:

,

        (1)

Угловая скорость УО

,

        (2)

где        R - плечо приложения усилия РМ к УО, R=3см;

      Sp, Vp - перемещение и скорость УО, приведенные к штоку гидроцилиндра (ГЦ)

                    привода короснимателя (ПК), рассчитываются, соответственно,  по формулам:

         (3)

         (4)

 где Fдеф – сила деформации, определяется из выражения:

                     

 

            (5)

где    S - перемещение штока относительно ГЦ ПК;

       СМ -  жёсткость системы, СМ = 30000 кгс/см;

lu - люфт в кинематической передаче от ГЦ к УО, lu = 0,05 мм

Fпоз вычисляется по формуле:

            (6)

где Мпов – момент сил, действующий на УО от взаимодействия с

                  обрабатываемой поверхностью.

Fдеб рассчитывается по формуле:

           (7)

где  Мдеб  –  момент дисбаланса от перегрузок.

          Mp  –  масса штока ГЦ с тягой к УО и приведённая к штоку ГЦ масса УО,

                     рассчитываемая по формуле:

           (8)

           где  Ip - суммарный момент инерции УО и штока ГЦ с тягой

                         к УО относительно оси вращения УО, Ip=10·10-4 кгс с2·м.

Скорость движения штока ГЦ описывается уравнением:

 

           (9)

где     Кд - коэффициент демпфирующей нагрузки на шток ГЦ, Кд = 1кгс·с/см.

Сила трения Fтр рассчитывается по формуле:

          (10)

где    Ктр   - безразмерный коэффициент сухого трения в ГЦ,  Ктр = 0,05;

 Fгц – с ила, действующая на шток ГЦ, описывается выражением:

          (11)

       где  А1 -  эффективная площадь поршня бесштоковой полости ГЦ, А1 = 10,48 см2;

    А2 - эффективная площадь поршня штоковой полости ГЦ, А2 = 1,16   см2;

Р1, Р2 – давление в бесштоковой и штоковой полостях ГЦ.

Перемещение штока ограничивается механическими упорами ГЦ, расстояние между которыми L = (1,6 – 0,01)см. При полностью втянутом штоке S = -Sвт (Sвт = -0,1) см. В точках механических упоров  = 0. Рабочий диапазон перемещения штока составляет от 0 до      12,7 мм и соответствует рабочим углам поворота УО от 0 º до 25º.

Давление Р1 и Р2 в формуле (11) определяются из уравнений:

          (12)

          (13)

 

          (14)

          (15)

где               Е - приведённый модуль упругости ПК, Е = 6000кгс/см2;

W1, W2 – объёмы бесштоковой и штоковой полости ГЦ;

  Q1, Q2 – расходы рабочей жидкости, поступающей в полости ГЦ или

                 вытекающей из них.

Зависимости объёмов W1, W2 от перемещений штока S имеют вид:

          (16)

          (17)

где W1n ,W2n -  «паразитные» объёмы бесштоковой и штоковой полостей ГЦ,

                          W1n = W2n = 3 см2.

Значения расходов Q1 и Q2 зависят от проводимостей рабочих окон и каналов золотникового распределителя и от перепадов давления на них:

 

          (18)

 

          (19)

          (20)

где Pвх - давление на входе золотникового распределителя Pвх = (255…295)кгс/см2;

      Pвх  - давление на выходе золотникового распределителя, Pвх ≤ 4кгс/см2;

       G3 – суммарная проводимость рабочего окна и канала золотникового

                распределителя, определяется из выражений:

G3 = 0, если  = 0;

          (21)

 

          (22)

где -  максимальная проводимость рабочего окна при (=1),

                     = 25,6 ;

             - проводимость канала золотникового распределителя,  = 210 ;

 - относительное перемещение золотника электрогидравлического

               усилителя (ЭГУ), безразмерное перемещение золотника  

               определяется выражениями:

 

           (23)

                  где   - относительное перемещение струйной трубки 1-го каскада ЭГУ;

                         -  относительное перемещение струйной трубки, при котором происходит

                                   насыщение силовой характеристики 1-го каскада,  = 0,7 … 1;

                            - постоянная времени золотника ЭГУ,  = от 2,5  до 3 мс;

                           - отношение силы от линейных перегрузок, действующих на золотник,

                                   к максимальной тормозной силе 1-го каскада ЭГУ.

   Относительное перемещение струйной трубки 1-го каскада ЭГУ вычисляется по формулам:

 

          (24)

         (25)

где  - относительный эквивалентный ток;

       - зона нечувствительности магнитоэлектрического преобразователя (МЭП)  ≤ 0,08;

       - относительный командный ток насыщения ,  = 0,25.

Относительный эквивалентный ток рассчитывается следующим образом:

          (26)

где  - относительный командный ток СУ;

      - смещение зоны нечувствительности магнитоэлектрического преобразователя (МЭП);

      - относительный командный ток насыщения ,  = 0.25 … 1.

Смещение середины зоны нечувствительности МЭП рассчитывается по формуле:

          (27)

где  - относительное смещение середины зоны нечувствительности МЭП                    от конструктивных факторов, .

        - относительное смещение середины зоны нечувствительности МЭП от линейных перегрузок (отношение момента дисбаланса подвижных частей МЭП при действии                 линейных перегрузок к максимальному моменту, развиваемому МЭП), определяется из выражения:

           (28)

где   n - коэффициент суммарной перегрузки;

        nmax  - коэффициент максимальной суммарной перегрузки, nmax = 200;

         - максимальное значение ,  = 0,09.

Отношение силы от линейных перегрузок, действующих на золотник, к максимальной тормозной силе 1-го каскада ЭГУ,  рассчитывается по формуле:

           (29)

где   - максимальные значения , ,  при этом

           (30)

Величина nmax зависит от ориентации ЭГУ на изделии.

Относительные перемещения и  определяются отношением их значений к соответствующим максимальным перемещениям.

Все относительные токи, зона нечувствительности и её смещение определяются по отношению к максимальному командному току ik max = 40мА. Значение силы командного тока изменяется в диапазоне от минус 40 до +40 мА.

Угол поворота вала кругового индукционного датчика обратной связи в зависимости от перемещения штока ГЦ определяется выражениями:

 

  (31)

 

  (32)

где   -   люфт в кинематической передаче от штока ГЦ к датчику обратной связи,

                 = 0,04 мм,;

    - плечо поворота вала датчика обратной связи,  = 2,4см,.

При смене направления движения штока вал датчика останавливается в пределах люфта.

При моделировании процесса работы гидропривода для дифференциальных уравнений математической модели задаются следующие начальные условия в момент

времени t = t0:

Предложенная математическая модель позволяет исследовать процесс работу механизма резания в процессе окорки лесоматериалов.

Преимущества модели в том, что наиболее точно учитываются различные нелинейности (люфты, дисбаланс, запаздывание, «паразитные» объемы, утечки и т.д.). При подобном подходе обеспечивается наибольшая точность моделирования процесса, корректность физического описания процессов обеспечивается развитым математическим аппаратом системы MatLab.

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Берстенёв А.В., Побединский В.В., Санников С.П. Система автоматического управления рабочими органами роторного окорочного станка. – Сборник докладов второй научно-техн. конф. молодых специалистов. – Екатеринбург:    УГЛТУ, 19 апреля 2006 г.

            2. Дорф Р.К., Бишоп Р. Х. Современные системы управления. – М.: «Лаборатория Базовых Знаний», 2004 г. – 832 с.

            3. Александров В.В., Болянский В.Г., Лемак С.С., Парусников Н.А., Тихомиров В.М. Оптимальное управление движением. – М.: «Физматлит», 2005 г. -375 с.

4. Пигильдин Н.Ф. Окорка лесоматериалов.–М.: Лесная промышленность,1982-192с.