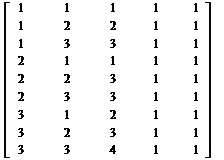Моделирование рабочих
процессов роторного
окорочного станка в
среде MatLab
Побединский В.В., Берстенев
А.В., Шуняев С.Н.
(УГЛТУ, г.Екатеринбург,
РФ) nto@krovtrade.ru
Modelling of
working processes on
rotary the debarking machine
in MatLab environment
Как известно [1], для исследования системы автоматического управления (САУ) рабочими органами роторного окорочного станка используются спектральные характеристики воздействий со стороны микропрофиля поверхности обрабатываемого лесоматериала. Динамические нагрузки обусловливаются пороками древесины (кривизна, сучки, овальность и т. д.), распределение которых описывается имитационной моделью [2], позволяющей статистически оценить поверхность обрабатываемого лесоматериала.
Однако функциональные зависимости, связывающие характеристики лесоматериалов, пороков древесины, режимов обработки с одной стороны, и параметры динамических нагрузок с другой, установить практически невозможно. Наиболее эффективным подходом к решению такой задачи будет применение теории нечетких множеств (ТНМ) [3].
Разработка модели на основе ТНМ может быть выполнена в различных системах программирования, например, Delphi, Builder и др. Но системы объектно-ориентированного языка имеют только возможности построения моделей нечеткого вывода, что требует значительных затрат при разработке. В настоящее время к стандартным системам создан ряд приложений для практического использования нечетких множеств, одна из них – это MatLab, которая обеспечена наиболее развитыми пакетами Simulink и Fuzzy Logic Toolbox [5].
Для реализации всех концепций нечеткого вывода – фаззификации, агрегирования, активизации или композиции подзаключений, аккумулирования правил, дефаззификации выходных данных предусмотрены специальные процедуры и функции, созданные в пакетах моделирования MatLab.
Систему нечёткого вывода можно разработать, используя пакет Fuzzy Logic Toolbox в интерактивном
режиме или в режиме командной строки. Такой способ разработки обладает большой
гибкостью и простотой реализации. Применение данного инструментария при
проектировании нечётких систем наиболее подходит для решения задач исследования
свойств системы, особенно если результатом функционирования нечёткой системы
являются параметры, обладающие строго определённым физическим смыслом. Однако
при проектировании сложных многоуровневых систем, строящихся по
каскадно-модульному принципу, требуется мощный, легко масштабируемый механизм с
высокой степенью абстракции. При таком подходе наиболее рационально
использовать подсистему визуального проектирования динамических процессов Simulink.
В системе MatLab реализованы следующие функции нечёткой логики:
1. 11 встроенных ФП (функций принадлежности) для построения термов нечётких переменных. Наиболее характерные из них:
-
двухсторонняя кривая Гаусса (gauss2mf);
-
колоколообразная
кривая (gbellmf);
- П-образная функция принадлежности (pimf);
- трапециевидная функция принадлежности (trapmf) и т.д.
2. Функции управления структурой данных системы нечёткого вывода FIS (Fuzzy Interference System). Этот набор функций реализует:
- добавление и удаление из системы нечёткого вывода FIS функций принадлежности, переменных и правил нечёткого вывода.
- дефаззификации ФП;
- выполнение нечёткого вывода в FIS;
- генерация поверхности вывода FIS;
- отображение структуры входа-выхода системы нечёткого вывода;
- возможность вывода свойств нечёткой системы и отображение графиков всех функций принадлежности соответствующей лингвистической переменной;
- загрузку и сохранение системы нечёткого вывода на диска.
3. Функции и программы дополнительных методов, а также взаимодействия с пакетом Simulink.
|
|
|
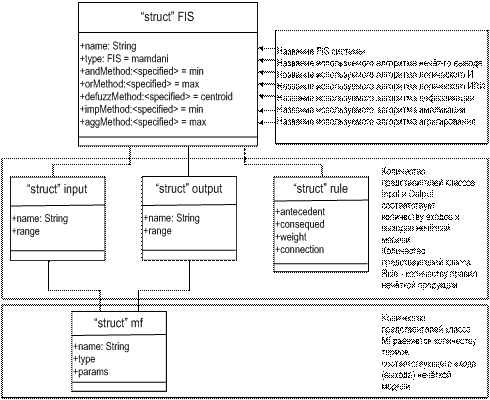
Рисунок 1 - Диаграмма классов структур системы нечёткого вывода |
Каждая система нечёткого вывода в MatLab представляется в виде специальной структуры, которая использует специальный цифровой формат. Данные системы хранятся структурировано и формируются в виде иерархии классов (см. рисунок 1). При этом все правила системы нечёткого вывода представляются в виде матрицы, содержащей одну или несколько строк (каждой строке соответствует отдельное правило). Если система нечёткого вывода имеет m входных и n выходных переменных, то соответствующая матрица должна иметь m+n+2 столбцов. Первые m столбцов относятся ко входным переменным, а следующие n – к выходным. При этом каждый столбец должен иметь номер, который должен соответствовать номеру функции принадлежности для выходной переменной. Столбец с номером m+n+1 содержит вес, с которым применяется данное правило. По умолчанию вес равен 1. Столбец с номером m+n+2 содержит число 1, если для подусловий данного правила используется нечёткий оператор AND (нечёткое И), 2 – если используется нечёткий оператор OR (нечёткое ИЛИ).
Так описания динамических нагрузок на режущий инструмент роторного окорочного станка зададимся следующими лингвистическими переменными, описывающими профиль обрабатываемой поверхности:
- переменная А – низкочастотная составляющая – описывает макронеровности вдоль оси лесоматериала (кривизна, величина сбега, овальность и т.д.);
- переменная В – высокочастотная составляющая – описывает микронеровности вдоль окружности лесоматериала (сучки, неровности, гниль, другие пороки).
Результатом использования нечёткой продукции является значение лингвистической переменная С – значение динамическая нагрузка на режущий инструмент.
Для системы нечеткого вывода строится база правил нечёткой продукции в виде нечетких лингвистических высказываний, например:
1. «ЕСЛИ В низкое и А низкое, ТО С низкое»;
2. «ЕСЛИ В низкое и А среднее, ТО С среднее»;
3. «ЕСЛИ В низкое и А высокое, ТО С высокое»;
4. «ЕСЛИ В среднее и А низкое, ТО С низкое»;
5. «ЕСЛИ В среднее и А среднее, ТО С высокое»;
6. «ЕСЛИ В среднее и А высокое, ТО С высокое»;
7. «ЕСЛИ В высокое и А низкое, ТО С среднее»;
8. «ЕСЛИ В высокое и А среднее, ТО С высокое»;
9. «ЕСЛИ В высокое и А высокое, ТО С очень высокое».
Правила нечёткой продукции в рабочей области MatLab представляются в виде матрицы:
|
|
|
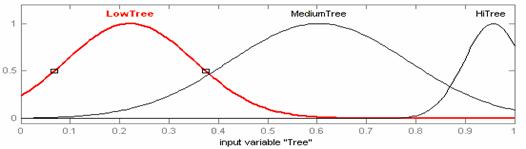
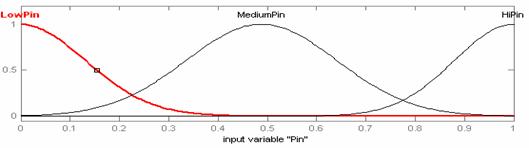
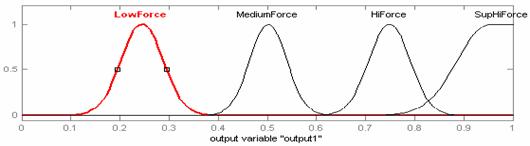
Графики термов лингвистических переменных показаны на рисунке 2.
Для реализации процесса нечеткого вывода используются блоки с несколькими входами. Поскольку база правил нечеткой продукции содержит большое количество нечетких высказываний, при этом с увеличением их количества точность вывода повышается, то организуется множество блоков. Если нечеткий вывод проводится на одном уровне блоков, то для продолжения вывода выходы блоков одного уровня связаны с входами на другом уровне, и в результате образуется структура нейролингвистической сети. Разработка таких сетей эффективно выполняется в системе Simulink и Fuzzy Logic Toolbox.
При разработке модели процесса окорки учитывалось, что поскольку База Данных всей системы (моделирование статистических параметров лесоматериалов, система нечетких высказываний) выполнены в Delphi, то в этой среде и организована оболочка программы.
Организации нечеткого вывода выполняются в пакете MatLab, с которым обеспечена синхронизация и обмен расчетными данными.
Работа со средствами НМ показала некоторые особенности приложений. Так пакет Toolbox целесообразно использовать для отработки в интерактивном режиме отдельных компонентов модели. Среда Simulink меньше приспособлена для таких целей, но в этом приложении может быть более эффективно выполнена разработка и отладка сложной математической модели объекта или многоуровневой нейролингвистической сети.
Теоретически предполагается, что в пакете MatLab количество уровней вложений не ограничено, однако это касается классических множеств, а для НМ сеть из пяти – шести уровней требует особой организации, так как добавление входных переменных увеличивает сложность вычислений экспоненциально и на практике становится уже не работающей. В этом случае необходимо разрабатывать особые средства, условия «обучения» сети, иначе программа начинает выполнять бесконечный цикл или выдаются данные с нулевыми результатами.
|
|
|
|
|
|
|
Рисунок 2 - Графики термов лингвистических переменных A, B, C. |
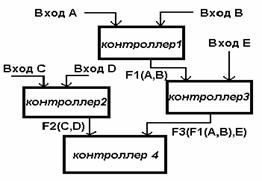
С учетом таких особенностей в модели предусмотрена организация не более трех уровней. При этом в среде Simulink для нечеткого вывода используется процедура обработки данных с помощью нечетких микроконтроллеров, объединенных вместе. Каждый элемент получившейся нечеткой сети обозначается как нечеткий узел. Выходы узлов одного уровня связаны с входами узлов другого, в результате все вычисления упрощаются. Этот подход можно назвать нечетким предвычислением (рисунок 3). Выходы нечетких узлов объединены с помощью мультиплексора, таким образом достигается более гладкий переход между множеством получающихся после обработки базы правил выводов.
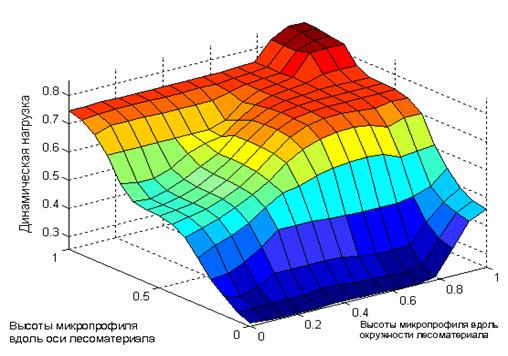
Основываясь на базе правил ТНМ, разработан алгоритм моделирования динамических нагрузок на механизм резания в процессе обработки лесоматериалов на РОС. В результате расчетов получена поверхность нечеткого вывода (рисунок 4) зависимости совместного влияния микропрофиля вдоль и по окружности лесоматериала на динамические нагрузки рабочего органа.
В процессе вычислений операции взятия минимума, максимума над нечеткими множествами, логические операции "И", "ИЛИ", "НЕ", производятся с помощью применения бинарных операций - t-норм или триангулярных норм к нечетким множествам. Последним этапом, дефаззификацией, является обратное преобразование результата, полученного в виде нечеткого множества, в числовое значение нечеткого вывода. Базовыми типами такого рода регуляторов используются контроллеры Мамдани и Суджено.
|
Рисунок 3- Нечёткие предвычисления |
|
Рисунок 5 - Поверхность картины нечёткого вывода динамических нагрузок |
Заключение
При создании моделей на основе теории нечеткого вывода наиболее приспособленной средой реализации являются приложения Simulink и Fuzzy Logic Toolbox системы MatLab. Наличие специальных средств позволяет эффективно выполнить разработку многоуровневых алгоритмов, в том числе организованных в виде нейролингвистических сетей.
Наиболее реалистичная модель рабочих процессов роторного окорочного станка может быть построена на основе двух различных методов - имитационного моделирования статистических параметров лесоматериалов и теории нечетких множеств, для получения процесса динамических нагрузок короснимателей. Такую структуру с Базой Данных рациональнее организовать в системе объектно - ориентированного языка с синхронизацией ядра программы с пакетом MatLab.
Полученные в результате моделирования по разработанному алгоритму процесса динамических нагрузок спектральные и амплитудные характеристики достаточно точно согласуются с экспериментальными данными, что говорит об адекватности модели.
Библиографический список
1. Берстенёв А.В., Побединский
В.В., Санников С.П. Система автоматического управления рабочими органами
роторного окорочного станка. – Сборник докладов второй научно-техн.
конф. молодых специалистов. – Екатеринбург: УГЛТУ, 19 апреля
2. Побединский В.В. и др. Имитационная модель процесса окорки
лесоматериалов на роторных окорочных станках. – В кн.: Вклад ученых и
специалистов в развитие химико-лесного комплекса. / Тез. докл.
к Обл. научно-техн. конф. – Свердловск, УЛТИ, 1-3 февраля
3. Берстенев
А.В., Побединский В.В., Шуняев С.Н. Применение
алгоритмов нечеткого вывода в моделировании объектов с нестрого определенными
параметрами. – В кн.: Ракетно-космическая техника. Научно-техн. сб. Системы управления ракетных комплексов. III науч.-техн.конф. молодых специалистов НПОА: -Екатеринбург:
Федер.аг. ФГУП
НПО «Автоматика» им. Академика Н.А.Семихатова, 9-11 апреля
4. Демидова Л.А., Кираковский В.В., Пылькин А.Н. Алгоритмы и системы нечеткого вывода при решении задач диагностики городских инженерных коммуникаций в среде MatLab. –М: Радио и связь, Горячая линия-Телеком, 2005 – 305 с.