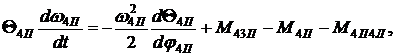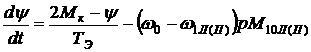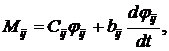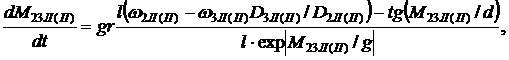МОДЕЛИРОВАНИЕ
МЕХАНИЗМА РЕЗАНИЯ ЛЕСОПИЛЬНЫХ РАМ С ПАРАЛЛЕЛЬНЫМИ СИЛОВЫМИ ПОТОКАМИ И
СИНХРОНИЗИРУЮЩИМ ЭЛЕМЕНТОМ
Кузнецов А.И., Новоселов В.Г., (УГЛТУ, Екатеринбург, РФ) akwer@yandex.ru
modeling of
the mechanism of log frames with parallel power streams and the synchronizing
element
KuzneTSov A.I., novoselov v.g. (USFEU, Ekaterinburg,
RU) akwer@yandex.ru
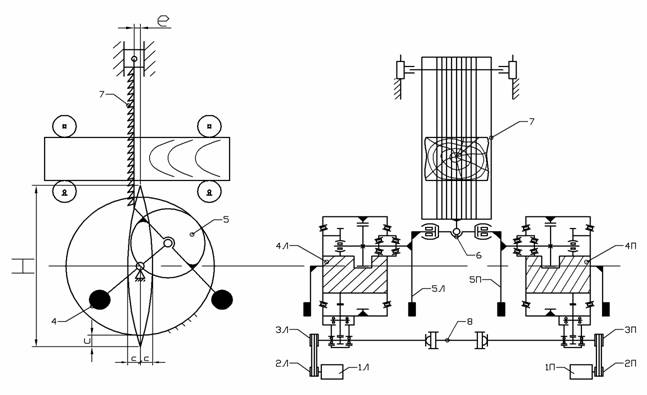
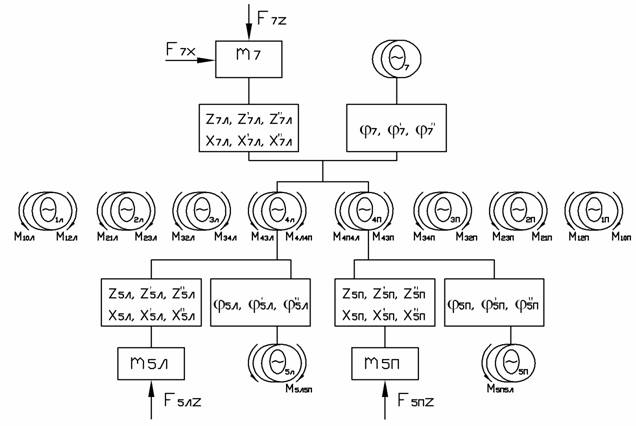
Важнейшим звеном в лесопильном производстве являются лесопильные рамы. Их существенным недостатком являются неуравновешенные силы инерции подвижных масс кривошипно-шатунного механизма, вызывающие вибрацию. Этот недостаток устранен в механизмах лесопильных рам (ЛРВ-2, РУН63) с планетарными преобразователями вращательного движения в возвратно-поступательное. Кинематическая схема механизма приведена на рисунке 1. На схеме индексами Л и П обозначены соответствующие симметричные элементы левого и правого преобразователей и их приводов.
|
|
|
Рисунок 1 - Кинематическая схема механизма резания лесопильной рамы с планетарным преобразователем: 1П,1Л – роторы электродвигателей; 2П,2Л - ведущие шкивы приводов; 3П,3Л - ведомые шкивы приводов; 4П,4Л – водила; 5П,5Л - сателлиты; 6 - траверса, 7- пильная рамка; 8 – синхронизирующий вал. |
В этих механизмах полностью уравновешиваются вертикальные и
горизонтальные силы, действующие на фундамент. Однако при смене скорости и
направления движения пильной рамки
происходит перекладка зазоров в зубчатых парах. Вследствие этого может
возникать ударная нагрузка на зубья и происходить их постепенное разрушение.
Кроме того, механизм имеет достаточно сложную структурную и
кинематическую схему, включающую два замкнутых силовых контура:
·
синхронизирующий вал – правый и левый преобразователи -
траверса пильной рамки;
·
синхронизирующий вал
– правый и левый приводы – электрическая сеть.
Ввиду различия механических характеристик асинхронных двигателей,
неравенства фактических передаточных отношений ременных передач и упругого
скольжения в них, кинематических погрешностей в зубчатых передачах планетарных
преобразователей неизбежно возникновение паразитных потоков мощностей и
дополнительных нагрузок на звенья механизма и его приводов. В частности, в
практике эксплуатации наблюдаются усталостные изломы синхронизирующих валов.
Учесть эти факторы и их влияние на динамические нагрузки и на
надежность механизма можно, имея адекватную динамическую модель. Для механизма
с планетарным преобразователем разработанная нами [1, 2] динамическая модель
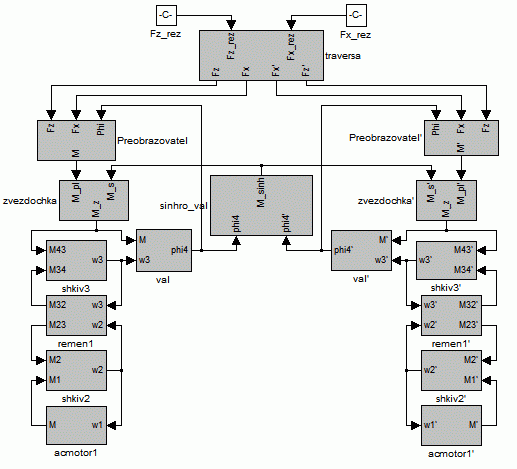
представлена на рисунке 2.
|
|
|
Рисунок 2 - Динамическая модель механизма резания лесопильной рамы с планетарным преобразователем |
Данная динамическая модель описывается системой дифференциальных
уравнений:
|
|
|
(1,2) |
|
|
|
(3,4) |
|
|
|
(5,6) |
|
|
(7) |
|
|
|
(8) |
|
где ΘiЛ, ΘiП – моменты инерции,
ωiЛ, ωiП и
φiЛ,
φiП
– угловые скорости и углы поворота вращающихся звеньев левого (Л) и правого (П) преобразователей и
приводов; MijЛ, MijП – реакции связей; M4Л, M4П – моменты сил сопротивления приведенные водилам.
Реакция нестационарной электромагнитной связи ротора и статора
двигателей приводов определяется из дифференциальных уравнений связи [3]:
|
|
(9) |
|
|
(10) |
где ω0 – угловая
скорость магнитного поля статора; p – число пар
полюсов статора; ТЭ – электромагнитная постоянная времени; ψ – вспомогательная переменная; MК – критический
момент двигателя.
Упруго – диссипативные реакции валов двигателей, синхронизирующего
вала и траверсы Mij определяются по
общей формуле:
|
|
(11) |
где Cij – коэффициент
жесткости упругой связи между i – тым и j – тым звеном; bij – коэффициент неупругого
(диссипативного) сопротивления связи между
i – тым и j – тым звеном; jij – угол
относительного поворота i – того и j – того звена.
Упругопластическая характеристика ременной передачи аппроксимируется
дифференциальным уравнением [4]:
|
|
(12) |
где d, g, l, r –
аппроксимирующие коэффициенты; D2Л(П), D3Л(П) – расчетные диаметры ведущего и ведомого
шкивов левого и правого приводов.
Поскольку, получить решение данной системы дифференциальных уравнений в аналитическом виде невозможно, будем исследовать данную модель методами численного моделирования.
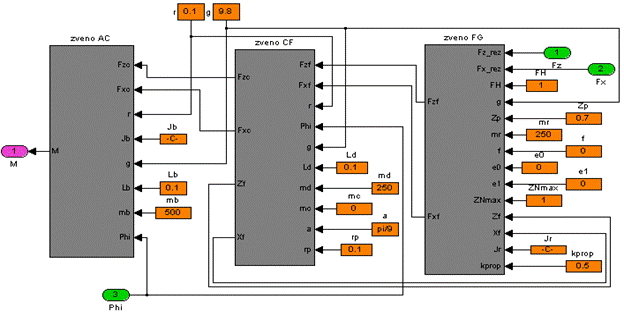
Для решения поставленной задачи удобно использовать пакет визуально-ориентированного программирования Simulink, входящий в состав системы Matlab. Модель механизма резания лесопильных рам с параллельными силовыми потоками и синхронизирующим валом представлена на рисунке 3.
|
|
|
Рисунок 3 - модель механизма резания |
Исследуемая модель представлена системой с входящими в неё подсистемами на рисунке 4, часть, которых, в свою очередь, содержит внутренние подсистемы. Каждая подсистема представляет собой самостоятельную структурную единицу и при необходимости может использоваться для исследования других моделей.
|
|
|
Рисунок 4 – Подсистема «Преобразователь» |
|
|
|
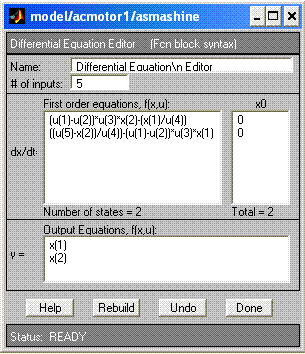
Рисунок 5 - Уравнения (6,7) в блоке Differential
Equation Editor |
Для обмена информацией между подсистемами, последние используют порты ввода и вывода. При моделировании механической модели удобно использовать для связи элементов такие параметры как момент и угловую скорость. Подсистемы, в математическом описании которых используются обыкновенные дифференциальные уравнения, могут моделироваться в специализированном блоке Differential Equation Editor (рисунок 5) в математическом виде. Среда Simulink содержит множество блоков для генерирования различных сигналов, среди них имеется блок «From File» с помощью которого задавались горизонтальные и вертикальные силы резания, полученные в результате натурного эксперимента из источника [5]. Для вывода результатов эксперимента используются средства: блоки «scope» и «XY Graph» – для отображения информации виде графика, блок «To File» - вывод результатов в файл и другие.
Экспериментирование над моделью, построенной в пакете Simulink, позволяет оперативно и наглядно представлять результаты численного эксперимента при изменении различных параметров и свойств модели, и тем самым определить оптимальное их сочетание.
Библиографический
список
1.
Новоселов В.Г, Кузнецов А.И Исследование модернизированного
планетарного механизма резания лесопильной рамы с гибким звеном.// Изв. вузов. Лесной журн., 2005, №3, - С.84-90
2.
Новоселов В.Г, Кузнецов А.И Динамическая модель механизма
резания лесопильной рамы с планетарным преобразователем.// Наука и образование
на службе лесного комплекса: Матер. меж. нар. науч.-практ. конф. Т.2. –
Воронеж: Воронеж. гос. лесотехн. акад., 2005.
– С. 99 – 103
3.
Левин А.И. Математическое моделирование в исследованиях и
проектировании станков. – М.: Машиностроение, 1978. – 184 с.
4.
Новоселов В.Г. Моделирование крутильно-вращательных
колебаний в приводе оборудования.// Виброакустические
процессы в оборудовании целлюлозно-бумажных производств. – Екатеринбург: УГЛТА,
1995. – С. 118-124.
5. Белошейкин В.С Улучшение эксплуатационных показателей бесфундаментных лесопильных рам.// Дис. канд. техн. наук: 05.21.05 – Л. 1988. – 232 с.
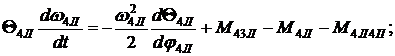 и
и