МОДЕЛИРОВАНИЕ ПРОЦЕССОВ
ДЕРЕВООБРАБОТКИ В УСЛОВИЯХ
НЕОПРЕДЕЛЕННОСТИ ПАРАМЕТРОВ СИСТЕМЫ
СТАНОК – ПРИСПОСОБЛЕНИЕ – ИНСТРУМЕНТ – ДЕТАЛЬ
Лялько А.А., Фридрих А.П., Кузьмицкий
И.Ф.
(БГТУ, г.
Минск, РБ) dosy@bstu.unibel.by
MODELING of WOODWORKING
PROCESSES In CONDITIONS
UNCERTAINTY of SYSTEM PARAMETERSN
THE RIG – thE ADAPTATION – thE TOOL – the DETAIL
Современные
математические методы и средства вычислительной техники позволяют решать
комплексные задачи анализа и синтеза электромеханических, гидромеханических,
пневмомеханических и других реальных систем с должной степенью полноты,
учитывая свойства всех входящих в общую систему узлов. Основная роль здесь
принадлежит методам математического моделирования.
Несмотря
на бесконечное многообразие конкретных конструктивных решений, реальные машины
и механизмы могут быть представлены в виде структур, состоящих из укрупненных,
агрегированных элементов, для которых известны и в той или иной мере исследованы
математические модели. Любую машину, в том числе и деревообрабатывающий станок,
при использовании системного подхода можно представить состоящей из следующих
элементов: преобразователя энергии (ПЭ); двигателя (Д); устройства передачи
движения (ЯД); рабочего процесса (РП); процесса рассеивания энергии (РЭ);
несущей системы (НС).
Рассмотрение
общей структуры объекта позволяет сделать вывод, что для эффективного
применения методов математического моделирования к исследованию и расчету машин
и механизмов различного назначения необходимо иметь типовые модели входящих в
эту структуру элементов и знать правила их соединения в общую систему. В этом
случае разнообразные задачи прикладной динамики машин обретают должную
методическую общность как в части постановки, так и в
части решения и интерпретации получаемых результатов.
Описание
механических процессов резания древесины состоит в выражении величин Yк,
характеризующих процесс, в виде функциональной зависимости от различных
переменных факторов хi. Зависимости Yк
= f(хi)
для многих процессов механической обработки древесины можно классифицировать
как:
1)
силовые – по условиям резания Fp = f(хi) и подачи Fп = f(хi), по мощностям
резания Рp = f(хi) и подачи Рп = f(хi);
2)
количественные – по неровностям поверхностей деталей; по ворсистости
поверхности W = f(хi); по точности размерообразований D = f(хi); по
предельной волнистости s = f(хi); по поперечной волнистости h = f(хi);
3)
технико-экономические – по себестоимости обработки С = f(хi), по производительности обработки П
= f(хi), по энергозатратам Э = f(хi).
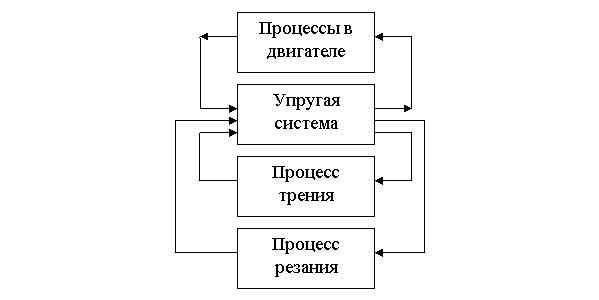
Рисунок 1 – Структурная схема дереворежущего станка
Учитывая,
что технологические процессы в деревообработке, в частности процессы резания древесины, не
поддаются точному теоретическому описанию, построение математических моделей
ведут с использованием статистическо-экспериментальных
методов. Для этой цели используют теорию планирования эксперимента. Применение активных и пассивных экспериментов позволяет
получить зависимость выходной
величины от различный воздействий у = f(хi) в виде уравнений регрессии. Это
особенно эффективно при оценке количественных и качественных показателей
технологических процессов деревообработки.
При
исследовании процесса резания фрезерованием были получены уравнения регрессии
для сосны, березы и дуба (в кодированных переменных).
Уравнение
регрессии для удельной силы резания в случае сосны (в кодированных переменных)
имеет вид:
Fs = 12.355 206 + 4.79 1148х(1) + .873 120x(2) +
– 1.431 000х(3) + 3.080 400x(4) +
+ 1.619 080x(5) + 1.170 000х(8) –
– .412 000x(9) – 0.484 500x(4)x(5) +
+ .702 000x(3)x(4) + 1.679 100x(1)x(4) +
– .682 080х(1)x(2) – 2.719 794х(1)2 –
– 1.215 000x(3)2 + .380 250x(4)2 – .739 840x(5)2 +
+ 1.130 000x(8)2,
где х(1) – средняя
толщина стружки; х(2) – плотность древесных
материалов; x(3) – угол перерезания волокон; х(4) – угол резания; х(5) –
радиус затупления режущей кромки; x(6) – скорость резания; х(7) – высота припуска; х(8) –
фаска на задней грани; х(9) – диаметр фрезерования.
Для
построения оптимальных систем управления необходимо получить динамические
характеристики процесса резания.
Найдем
изменение удельной силы резания во времени при линейном законе изменения
радиуса затупления для случая сосны.
Изменение
радиуса затупления резца имеет вид [1]
r = r0 + Dr,
где r0 – начальный радиус затупления.
Dr = gL,
здесь L – путь контакта; g –
прирост Dr на
Для
кругового резца
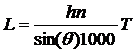 ,
,
где h – высота пропила, мм;
n – число
оборотов в минуту; q – средний кинематический угол
встречи; Т – чистое время на резание без потерь.
Скорость
резания, м/с:
![]() ,
,
где D – диаметр окружности резания.
Задав
номинальные значения g, L, h и варьируя v в определенных пределах,
получим передаточные функции силовых параметров:
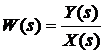 ,
,
где Y(s) – преобразованный по Лапласу выходной
сигнал (сила резания);
X(s) – преобразованный по Лапласу входной сигнал (скорость резания).
В
результате моделирования в пакете Маtlab были получены
передаточные функции силовых параметров на основе метода трапеций.
Силовые
параметры будем оценивать по току, потребляемому электродвигателем. Исходя из
этого, модель процесса резания может быть представлена в виде
I = kрезvh,
где I – ток, потребляемый
электродвигателем; v
– скорость резания; h – глубина резания; kрез – коэффициент пропорциональности.
Датчик
обратной связи будет описываться уравнением
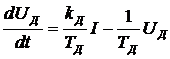 ,
,
где UД – напряжение на выходе датчика; kд, ТД – коэффициент
передачи и постоянная времени датчика.
Однако
следует заметить, что процесс резания является стохастическим, а это обусловлено
воздействием ряда возмущающих воздействий на систему станок - прибор -
инструмент - деталь (СПИД). Возмущающими воздействиями могут
быть: для элемента «станок» - подача, скорость, глубина резания, температура;
для элемента «приспособление» - геометрическая точность, жесткость, точность
установки; для элемента «инструмент» - точность, жесткость, износ, затупление; для элемента «деталь» - плотность, влажность,
механические свойства.
Большинство
из этих возмущений неконтролируемые и относятся либо к «внутренним»
возмущениям объекта (процесса резания), либо связаны с измерительной системой.
Кроме
того, некоторые параметры системы СПИД имеют скачкообразный характер изменения,
что накладывает дополнительные требования при моделировании процесса резания.
Таким
образом, целесообразно представить систему, адекватно описывающую процесс резания,
в виде стохастических уравнений в пространстве состояний.
Для
моделирования была выбрана передаточная функция для силы резания следующего
вида:
![]() .
.
Тогда
стохастическая модель системы в пространстве состояний будет
имеет вид [2]:
X(k
+ 1) = 0.9957X(k, s(k), s(k +1)) + 0.25U(k) + FN1(k),
Z(k) = CX(k) + EN2(k),
где X(k) – n-мерный вектор в пространстве состояний;
Z(k) – вектор наблюдений; f[k +1, s(k +1)] – вектор шумов наблюдения; N1(k), N2(k) – вектора гауссовских
случайных процессов; F, N – некоторые известные функции своих аргументов; U(k) – вектор управления, k = 0, 1..N – индекс дискретизации по времени; s(k) – вектор состояний структуры,
имеющий 2 состояния: С = 0.2892 при s = 1; С =1.5×0.2892 при s = 2.
В
нашем случае Х(k) - сила резания; Y(k) -скорость резания.
Оценки
для вектора X будем искать на основе алгоритма оптимальной фильтрации [3].

Рисунок 2 – Изменение структуры объекта и оценка изменения структуры
объекта
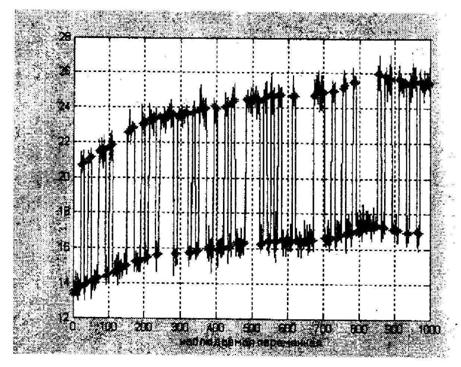
Рисунок 3 – Наблюдаемая переменная и её оценка
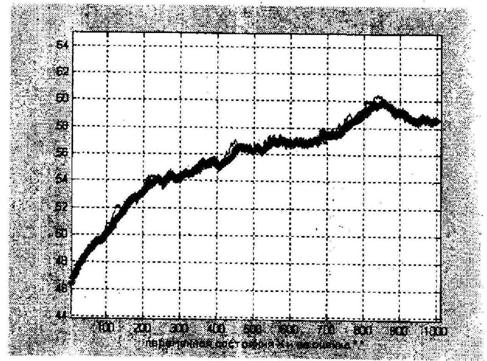
Рисунок 4 – Вектор состояния и его оценка
Таким
образом, алгоритм оптимальной фильтрации позволяет эффективно оценить вектор
состояния системы СПИД в условиях скачкообразного изменения ее параметров.
Библиографический список
1. Бершадский А. Л. Расчет режимов резания древесины. - М.:
Лесная промышленность, 1967.
2.
Пугачев В. С., Синицин И. Н. Стохастические
дифференциальные системы. Анализ и фильтрация. - 2-е изд., доп. - М.: Наука,
1990.
3.
Богуславский И. А. Прикладные задачи фильтрации и управления. - М.: Наука,
1983. - 400 с.