ДИНАМИЧЕСКОЕ МОДЕЛИРОВАНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ЭЛЕМЕНТОВ АКСИАЛЬНО-ПОРШНЕВЫХ ПНЕВМОМОТОРОВ
РАЕВСКАЯ Л. Т. (УГЛТУ, г.Екатеринбург, РФ) raevskaya@usfeu.ru
Dynamic modelling of the is intense-deformed condition
of elements axial-piston air motors
1. Описание конструкции аксиально-поршневого
пневматического двигателя типа ДАР
Из
аксиально-поршневых моторов многократного действия наибольшее применение в
машиностроении лесного и горного комплекса нашли реверсивные
аксиально-поршневые пневматические двигатели (пневмомоторы) типа ДАР с синусоидальным
кулачковым диском ротора [1]. Двигатели ДАР имеют бесшатунный механизм
преобразования возвратно–поступательного движения поршней во вращательное
движение выходного вала ротора.
Динамический момент создается поршнями двухстороннего действия, каждый
из которых имеет два подшипника, охватывающих синусоидальную профильную дорожку
ротора. Двухсторонний профиль ротора очерчен огибающими кривыми, положение
которых определяется дугами радиусов шлифовальных кругов при движении их
центров по двум эквидистантным (на расстоянии dш) синусоидальным
кривым. Сжатый воздух по воздухораспределительным каналам шейки ротора
поступает в поршневые полости и создает усилие, которое через подшипники
поршней передается на профильную дорожку ротора, приводя к появлению
динамического момента.
|
|
Поршни двустороннего действия расположены в двух частях блока цилиндров и через ролики (наружное кольцо подшипника) взаимодействуют с синусоидальным профилем центрально расположенного кулачкового диска ротора. Число волн синусоиды диска задает кратность хода поршней. За время одного оборота ротора поршень делает три двойных хода.
Для более равномерного вращения ротора вдоль периферии
кулачкового диска устанавливают несколько поршней. Соосное расположение поршней и выходного вала
позволяет снизить габариты и массу пневмомоторов. Эти двигатели по сравнению с
радиально-поршневыми той же мощности имеют в полтора-два раза меньшие габариты
и массу
Преимуществами аксиально-поршневых пневмомоторов
являются не только малые габариты, но и
отсутствие загрязнения окружающей среды, высокая безопасность работы. Это
обуславливает перспективность их применения в приводах технологических машин
различного назначения.
1. Постановка задачи
Вместе с тем, опыт эксплуатации пневмомоторов на
предприятиях показывает, что основные отказы в двигателе - 80% - приходятся на
поршни и носят усталостный характер. Трещины появляются в зоне отверстия для пальца, на котором находится ролик, а также в
области паза, через который проходит волнообразная поверхность торца
кулачкового диска.
Как нами было получено, вблизи отверстий в теле поршня
появляется концентрация повышенных напряжений, причем наибольшие из них могут в
несколько раз превышать так называемые «средние напряжения» [2]. Недостаточное
знание истинной картины напряженного состояния может привести к перетяжелению
несущей конструкции или к разрушению. Поэтому проблеме концентрации напряжений
уделяется большое внимание.
В настоящей работе рассматривается задача инженерного
моделирования прочностной надежности элементов поршня и расчета
напряженно-деформированного состояния при статическом нагружении с помощью
программного комплекса ANSYS.
2. Математический аппарат
Математической
основой, на которой построен вычислительный аппарат программного комплекса ANSYS, является метод конечных элементов
(МКЭ), наиболее распространенный и достаточно универсальный метод анализа
напряженно-деформированного состояния. В этом методе нет ограничений ни на
форму тел, ни на способ приложения нагрузки. Основными моделями прочностной
надежности, которые всегда присутствуют при проведении расчетов, являются
модели материала, формы конструкции, условий нагружения, предельного состояния
[3].
3. Результаты предыдущего расчета
Нами уже была предпринята попытка расчета поля
напряжений в роторно-поршневой группе пневмомотора с использованием МКЭ
[2]. Решение задачи численного анализа
параметров режимов нагружения пневматического двигателя было выполнено в
системе РС MatLAB, позволяющей работать с разряженными матрицами. Был
разработан комплекс программ, который включал программы разбиения тела на
конечные элементы, построения глобальной матрицы жесткости, учета граничных
условий, вычисления напряжений, представления результатов расчетов.
Однако сделанные в работе [2] приближения:
1. поршень рассмотрен как цилиндрическая
поверхность с заданным распределением отверстий определенной конфигурации;
толщиной поршня пренебрегалось;
2. в качестве первого шага к расчету
напряжений была сделана развертка поршня в деталь плоской формы; для расчета
выбрана четверть развертки;
3. нагрузка была приложена вдоль линии
пересечения торца поршня и цилиндрической поверхности
не позволили в
полной мере получить картину поля напряжений в поршне, хотя вблизи отверстия
был получен результат, совпадающий с теоретическими оценками.
Концентрация напряжений
возрастала вблизи отверстий и достигала максималных значений 857,9 Па в области
контакта поршня и пальца.
Область напряжений вблизи
отверстия для пальца представлена на рис. 2.
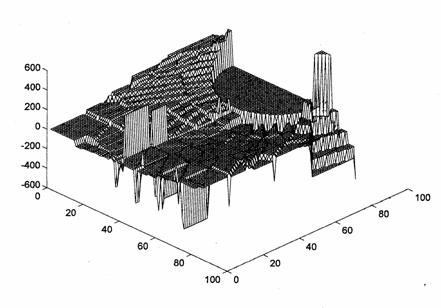
Рис.2 Поле напряжений в области контакта пальца с
поршнем.
4. Моделирование динамических процессов
Расчет
динамических нагрузок, напряжений и усталостной долговечности в элементах
поршня дает возможность точнее подобрать их параметры, добиться более полного
соответствия динамических характеристик элементов поршня поставленным
требованиям. Моделирование динамических процессов в роторно-поршневой группе с
учетом упругой деформации и демпфирования поршня позволяет уточнить картину
нагружения поршня и исследовать характер действующих в нем сил.
Для
моделирования механическая система заменена эквивалентной ей колебательной
системой, для которой составлено уравнение движения. После решения уравнения
исследовано влияние параметров (коэффициентов) на поведение системы. В
результате анализа решена проблема оптимизации параметров, исходя из картины
динамического нагружения [4].
Колебательная
система, эквивалентная поршню в сборе с пальцем и роликом - это точечная масса
m (равная массе поршня), связанная с ротором с помощью пружины и вязкого
демпфера, моделирующие упругие свойства данной механической системы. Жесткость
диска ротора в первом приближении не учтена.
При
динамическом режиме работы системы выходная величина - ускорение поршня -
непрерывно меняется со временем, и вид функции a(t) зависит от типа внешнего
воздействия и собственных динамических свойств системы. Внешнее воздействие в
данном случае - это давления в рабочей камере P1(t) и камере выхлопа P2(t),
которые сами являются переменными величинами. Динамические процессы в общем
случае описываются дифференциальными уравнениями.
Уравнение
движения поршня вдоль оси Х, совпадающей с осью поршня, составлено в виде
![]() (1)
(1)
где m -масса
поршня, x(t), xo(t) -
координаты верхней точки головки деформируемого и недеформируемого поршня, соответственно;
(x'-xo')- скорость относительного движения этой точки, d - диаметр
поршня, c - коэффициент жесткости, b – коэффициент демпфирования, характеризует
вязкие свойства поршня, P1(t), P2(t) - давление в камере наполнения
и камере выхлопа соответственно. Из закона движения центра ролика поршня в
параметрическом виде и соотношения для расстояния от стенки цилиндра до точки,
отстоящей от верхней точки профиля ротора на величину 0,5(dш-H), где dш – расстояние между центрами
шлифовальных кругов, H - ход поршня, получили формулу для xo, а
именно
![]() (2)
(2)
Здесь lН-
начальный зазор между поршнем и торцовой стенкой цилиндра, j(t)- текущий
угол синусоиды профиля ротора, Rш- радиус шлифовального
круга, Rр- радиус ролика, Dср- средний
диаметр волны ротора, A параметр, зависящий от числа волн синусоиды n
A = (n2 H2
Sin2j(t)+DСР2)1/2 . (3)
Была уточнена
картина нагружения поршня и исследован характер действующих в нем сил. Исходя
из картины динамического нагружения, были оценены коэффициенты жесткости элементов
поршня в области линейных деформаций, подобран коэффициент демпфирования.
6.
Расчет
поля напряжений. Объемная задача
Опубликованные
в [4] результаты использованы в настоящей работе для вычисления напряжений в
теле поршня методом конечных элементов.
Внешние
воздействия, распределенные вдоль поверхности торца поршня, приняты равными
сумме статической нагрузки от давления воздуха в магистрали и динамической
составляющей [4]. Расчетное значение полной нагрузки с учетом динамической
составляющей для пневмомотора ДАР-14М получилось равным 5480 Н. Давление в
магистрали газораспределительной системы 0.5 *106 Н/м2. Жесткость
системы С равна 1.39 * 109 Н/м.
При расчете
использована упрощенная твердотельная модель поршня пневмомотора. Не учтены
радиусы скруглений в сопряженных стенках, некоторые мелкие выемки и пазы для
поршневых колец (уплотнителей), небольшие отверстия и пр.
Геометрическая модель поршня была построена путем вращения на задаваемые
углы фигур простых форм (геометрических примитивов). Этот шаг оказался наиболее
трудоемким. Конечно-элементная модель поршня выполнена из объемных
тетрагональных элементов с 10 узлами SOLID 92 с помощью произвольной сетки,
которая построена автоматически. Поскольку поршень имеет плоскость симметрии, то для уменьшения трудоемкости
задачи было принято решение рассмотреть половину детали, что сократило число
элементов почти вдвое (теперь это число
приняло значение порядка 24000).
|
|
Рис.4 Упрощенная геометрическая модель поршня |
Материал поршня – изотропный с постоянными свойствами. В расчете приняты
следующие характеристики материала. Модуль упругости Е взят равным ![]() Па, коэффициент
Пуассона – 0.3.
Па, коэффициент
Пуассона – 0.3.
В качестве
первого шага при решении прочностной задачи было решено определить только поле
напряжений, собственные частоты колебаний будут определены позднее.
Схема
закрепления. Запрещено движение сечения поршня плоскостью симметрии в
направлении, перпендикулярном данному сечению. Кроме того, ограничено движение
внутренней поверхности касания пальца и поршня с одной стороны поршня.
7. Результаты
В качестве результата задаем выдачу следующей информации:
изменение формы поршня, наибольшее абсолютное смещение вдоль оси поршня,
максимальное значение напряжения вдоль оси поршня, поле напряжение в режиме анимации.
Полученные максимальные и минимальные значения приведены в табл. 1.
Теоретические
оценки напряжений по оси Х дали значения ![]() .
.
Как видно из
таблицы, расчетные данные совпадали с оценочными.
Изменение
формы в виде анимации дает возможность увидеть сам процесс деформации. Наибольшее
смещение происходит в точках на границе паза под ротор. Наибольшие напряжения
возникают в областях опоры под палец смежных с торцом цилиндра и с ребром
жесткости.
Таблица 1. Абсолютные смещения (мм), напряжения (Н/м2)
и реакции (Н) в узлах в системе глобальных координат
|
=================================================================================== THE
FOLLOWING DEGREE OF FREEDOM RESULTS ARE IN GLOBAL COORDINATES
NODE UX UY UZ MAXIMUM ABSOLUTE VALUES NODE
2212 2232 11866 VALUE -0.14519E-02-0.19792E-02 0.27803E-03 =========================================================================================
***** POST1 NODAL STRESS LISTING ***** THE
FOLLOWING X,Y,Z VALUES ARE IN GLOBAL COORDINATES
NODE SX SY SZ SXY SYZ SXZ MINIMUM VALUES NODE
1391 1281 11849 18352 11849 12416 VALUE
-0.51190E+07-0.34239E+07-0.30295E+07-0.18932E+07-0.10384E+07-0.82329E+06 MAXIMUM VALUES NODE
572 11609 1295 13443 18200 14229 VALUE 0.42853E+07 0.25226E+07 0.20933E+07
0.20277E+07 0.64693E+06 0.21313E+07 ========================================================================================= PRINT REACTION SOLUTIONS PER NODE
***** POST1 TOTAL REACTION SOLUTION LISTING *****
THE FOLLOWING X,Y,Z SOLUTIONS ARE IN GLOBAL COORDINATES
NODE FX FY FZ TOTAL VALUES VALUE 0.12629E+10 0.61257E-03-0.60885E+09 |
На рис. 5-11
приведены графические результаты решения задачи.
|
|
|
|
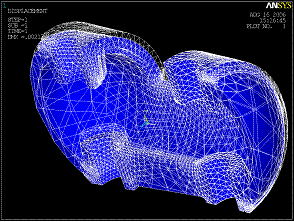
Рис.5 Совмещенные
изображения половины поршня до и после приложения нагрузок в пространстве |
Рис.6. Совмещенные изображения половины поршня до и после
приложения нагрузок в пространстве в плоскостях XY |
На рис.6 указано максимальное значение смещения по оси х; видно, что сильно смещена внутренняя поверхность отверстия под палец, к которой не были приложены граничные условия.
|
|
|
|
|
а) |
б) |
|
|
Рис. 7. Совмещенные изображения половины поршня до и после приложения нагрузок в пространстве (а) и в плоскостях XZ (б), с указанием максимального значения смещения по оси х |
||
Видно, что сильно смещена внутренняя поверхность отверстия под палец, к которой не были приложены граничные условия.
|
|
|
|
|
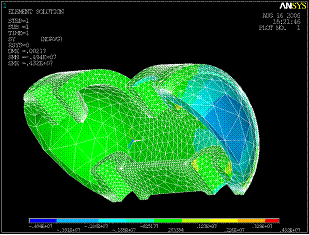
Рис. 8 |
Рис. 9 |
Рис. 10 |
На рис.8-10 показано трехмерное цветное изображение поля нормальных напряжений в плоскостях перпендикулярных осям Х и У, на полях рисунков показаны максимальные и минимальные значения напряжений с указанием номеров соответствующих элементов.
|
|
|
|
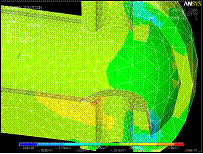
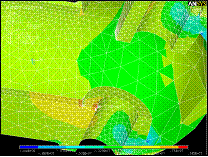
На увеличенном изображении опоры под палец с полем напряжений в цвете отчетливо видна область красного цвета (растяжение) на внутренней части опоры и в районе контакта с ребром жесткости и область темно-синего цвета (сжатие) на противоположной стороне опоры.
На
усредненном поле напряжений без сетки (рис. 11) видно, что угол паза также
испытывает деформацию растяжения, превышающую средние значения, так что можно
рекомендовать конструктивно изменить форму паза, сделав, например выточку в
углу, чтобы убрать концентратор напряжений в этих точках.
СПИСОК
ЛИТЕРАТУРЫ
1. Зинкевич В. Д., Ярмоленко
Г. З., Калита Е. Г. Пневматические двигатели горных машин. М.: Недра.1975
г., 344 с.
2. Раевская Л.Т. Исследование поля напряжений
в теле поршня пневматического двигателя. Сб. тезисов докладов Международной
научно-технической конференции. Т.1, с.318-319, 3-4, ноябрь, 2004, Государственный
технический университет, Архангельск.
3. Каплун А. Б., Морозов Е. М.,
Олферьева М. А. ANSYS в руках инженера: Практическое руководство. Изд. 2-е, испр.
М.: Едиториа УРСС, 2004.-272 с.
4. Раевская Л. Т., Анкудинов
Д. Т., Карякин А. Л. Моделирование динамических процессов в пневматическом
двигателе привода горных машин. Сб. докладов 12-й международной конференции по
автоматизации в горном деле IСАМС’95, стр. 537–540. 13–15, сентябрь 1995, Силезский
технический университет, Гливице, Польша.

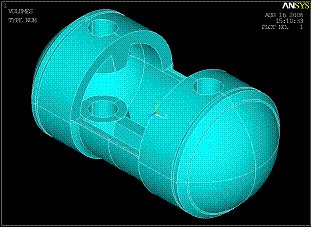 Рис.3
Полная геометрическая модель поршня
Рис.3
Полная геометрическая модель поршня