О  КОНВЕКТИВНОМ  ТЕПЛООБМЕНЕ  РЕЖУЩЕЙ  ЧАСТИ  ПИЛЫ  ПРИ  РЕЗАНИИ

 

Пашков В.К., Щепочкин С.В. (УГЛТУ, г. Екатеринбург, РФ)    art-sit@yandex.ru

About convective  HEAT  EXCHANGE  of  a  CUTTING PARTSAWS  AT  CUTTING

 

В работах по исследованиям теплофизической обстановки в зоне резания круглыми пилами, оценки доли тепла, отводимого через инструмент существенно различаются. По результатам экспериментальных исследований [1] через контактные поверхности лезвий зубьев с древесиной на нагрев пил расходуется до 70 % общего количества эквивалентной тепловой мощности при резании. При этом 60…65 % идёт на нагрев режущей части пилы в установившемся тепловом режиме.

Для аналитической оценки количества тепла, расходуемого на нагрев режущей части необходимо знать достоверную информацию о распределении температуры по высоте зуба и коэффициенте теплоотдачи зуба при конвективном теплообмене с окружающей средой.

По нашим исследованиям температурный напор данного сечения зуба по высоте над температурой окружающей среды определяется выражением

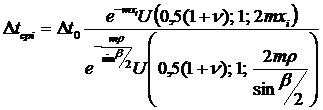,                        (1)

где       Dt0 – превышение температуры резания над температурой окружающей среды, оС;

            e – основание натурального логарифма, e = 2,71828;

             – конфлюэнтная (вырожденная) гипергеометрическая функция 3-х аргументов 0,5(1+n); 1 и 2mxi;

b – угол заострения зуба, град.;

xi – расстояние от вершины зуба до рассматриваемого участка, м;

r – радиус затупления лезвия, м;

            m и n – коэффициенты, необходимые для нахождения аргументов гипергеометрической функции, которые соответственно равны

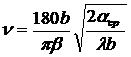;    ,                                            (2)

где       aср – коэффициент теплоотдачи зуба в окружающую среду, Вт/(м2 оС);

            l – коэффициент теплопроводности материала зуба, Вт/(м оС).

b – толщина зуба (пильного диска), м;

Коэффициент конвективной теплоотдачи aср при принятых скоростях вращения пил, устойчивом турбулентном перемещении потоков воздуха и его независимости от ширины пропила определяется выражением [2]

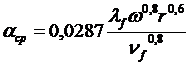,                                              (3)

где       lf  – коэффициент теплопроводности воздуха, lf  = 2,59×10-2 Вт/(м×оС);

            w – угловая скорость вращения диска, рад/с;

            r – радиус пилы, м;

nf – кинематическая вязкость воздуха, nf = 15,06×10-6 м2/с.

Для определения теплоты, передающейся в окружающую среду режущей частью (зубьями) пилы QОКР условно зуб пилы разбиваем на кольцевые участки радиусом хi и шириной Dx (рисунок 1). На каждом из них теплоотдача в окружающую среду определяется по закону Ньютона-Рихмана

 

,                                                  (4)

где       z – число зубьев пилы;

Fi – площадь поверхности теплоотдачи участка, м2;

n – количество участков, 1, 2 … n.

Площадь поверхности теплоотдачи участка определяется из выражений:

 

для xi £ a 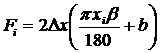                               ;                                         (5)

 

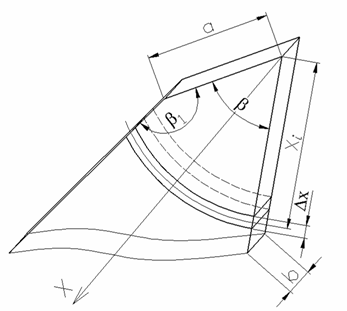
Рисунок 1 – Схема разбивки зуба по высоте на участки

 

для a £ xi £ h 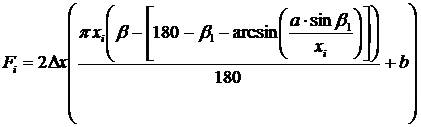    ,         (6)

где       Dx – ширина кольцевого участка, м;

            xi – расстояние от вершины зуба до рассматриваемого участка, м;

b – угол заострения зуба, град.;

b1 – вспомогательный угол, град.;

a – длина задней грани зуба, м;

b – толщина зуба (пильного диска), м;

h – высота зуба в направлении биссектрисы угла заострения b, м.

Подставив выражения (1) и (6) в формулу (4), получим

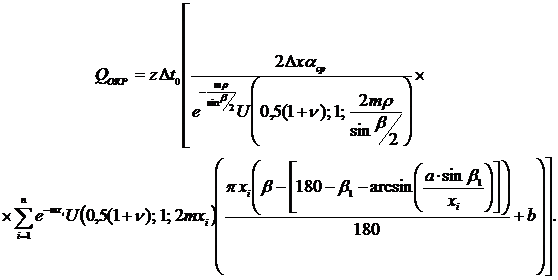   (7)

Выражение в квадратных скобках формулы (7) обозначим как aZ, Вт/ оС. Тогда

QОКР = z Dt0 aZ.                                                                    (8)

Величина aZ называется среднеинтегральным коэффициентом теплоотдачи зуба пилы. Она численно равна количеству теплоты, передаваемой зубом пилы в окружающую среду при повышении температуры резания на 1 оС в установившемся тепловом режиме.

Рассмотрим пример расчета среднеинтегрального коэффициента теплоотдачи зуба круглой пилы (ГОСТ 980-80 тип 1, исполнение 1) диаметром D = 500 мм, толщиной b = 2,5 мм, числом зубьев z = 60, при принятом коэффициенте теплопроводности материала зуба l = 37,8 Вт/(м оС). Частота вращения пилы n = 3000 мин-1 (w = 314 рад/с).

Для данной пилы, согласно [3] шаг зубьев tз = 26,2 мм, высота зуба составит h » 0,5tз » 13 мм, длина задней грани зуба а » 0,4tз » 10,5 мм, угол заострения b = 40о, угол b1 » 165о. Радиус затупления лезвия принимаем r = 10 мкм.

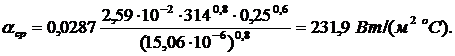
Условно зуб разбиваем на n = 13 кольцевых участков (рисунок 1), шириной      Dx = 1 мм. Подставим значения lf, w, r и nf в формулу (3) и определим средний коэффициент теплоотдачи зуба пилы

Коэффициенты m и n для принятых значений aср, l, b и b соответственно по формулам (2) будут равны

;   .

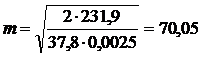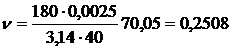Первый аргумент гипергеометрической функции U равен

0,5(1+n) = 0,5(1+0,2508) = 0,6254.

 Постоянную часть выражения aZ обозначим через P. Она будет равна

 

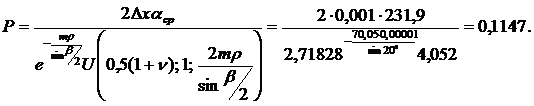
Переменную часть выражения aZ обозначим через S

 

Результаты расчета переменной части выражения aZ приведены в таблице 1.

 

Таблица 1 – Расчет среднеинтегрального коэффициента теплоотдачи зуба пилы

 

i

xi, мм

xi, м

z = x×m

e-z

U(0,6254;1;2z)

Dti

Si

0

0,0292

2,92×10-5

0,0020

0,998

4,052

1,000

-

1

0,5

0,0005

0,0350

0,966

2,167

0,517

0,0059612

2

1,5

0,0015

0,105

0,900

1,525

0,339

0,0048689

3

2,5

0,0025

0,175

0,839

1,258

0,261

0,0044838

4

3,5

0,0035

0,245

0,783

1,097

0,212

0,0042442

5

4,5

0,0045

0,315

0,730

0,984

0,178

0,0040506

6

5,5

0,0055

0,385

0,680

0,900

0,151

0,0038803

7

6,5

0,0065

0,455

0,634

0,833

0,131

0,0037189

8

7,5

0,0075

0,525

0,591

0,779

0,114

0,0035624

9

8,5

0,0085

0,596

0,551

0,733

0,100

0,0034094

10

9,5

0,0095

0,666

0,514

0,694

0,088

0,0032593

11

10,5

0,0105

0,736

0,479

0,661

0,078

0,0031123

12

11,5

0,0115

0,806

0,447

0,631

0,070

0,0028932

13

12,5

0,0125

0,876

0,417

0,605

0,062

0,0026934

SSi = 0,0502

Переменная часть выражения aZ составит S = 0,0502, а среднеинтегральный коэффициент теплоотдачи зуба пилы будет равен

 

aZ = P×S = 0,1147×0,0502 = 5,75·10-3  Вт/оС.

 

В таблице 1 расчеты выполнены для относительных температур по высоте зуба, т.е. их долей от значения температур вершины зуба t0, принятой за 1.

Для принятого диапазона значений параметров aср, b, h, b, b1 и а, влияющих на величину среднеинтегрального коэффициента теплоотдачи зуба пилы aZ, её аналитическая зависимость из формулы (7) аппроксимирована.

Зависимость aZ от высоты зуба h аппроксимирована полиномом 3-ей степени, а влияние остальных параметров aср, b, b, b1 и а аппроксимировано степенной функцией

,   (9)

где       b – толщина зуба (пильного диска), мм;

            b – угол заострения зуба, град.;

            aср – коэффициент теплоотдачи зуба в окружающую среду, Вт/(м2 оС);

b1 – вспомогательный угол, град.;

a – длина задней грани зуба, мм;

h – высота зуба в направлении биссектрисы угла заострения b, мм.

Разработанная зависимость (9) позволяет определять среднеинтегральные коэффициенты теплоотдачи зуба, не прибегая к сложному математическому аппарату. Коэффициент корреляции r = 0,976.

Таким образом, зная температуру резания, среднеинтегральный коэффициент теп­лоотдачи зуба aZ и число зубьев Z, по формуле (8) можно рассчитать количество теплоты, отводимое режущей частью пилы в окружающую среду теплоотдачей.

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Конов В.Н. Исследование влияния тепловых явлений на работоспособность круглых пил: автореф. дисс. … канд. техн. наук: 13.00.01/ Конов Виктор Николаевич; ЛТА. – Л., 1979, – 26 с.

2. Пашков В.К. Тепловое поле вращающегося охлаждаемого диска пилы / В.К. Пашков, А.С. Красиков // Деревообрабатывающие станки, инструменты и вопросы резания древесины. – Л.: ЛТА, 1984, С. 48 – 51.

3. Библиографическое описание документа: ГОСТ 980-80. – Взамен ГОСТ 980-69; введ. 01.01.1982. – М., 1999. – 25 с.