ОБ ОЦЕНКЕ ТЕМПЕРАТУРЫ РЕЗАНИЯ ПРИ ПИЛЕНИИ КРУГЛЫМИ ПИЛАМИ

 

Щепочкин С.В. (УГЛТУ, г. Екатеринбург, РФ) art-sit@yandex.ru

 

About an ESTIMATION of CUTTING TEMPERATURE AT SAWING by CIRCULAR SAWS

 

Установление законов распределения и численных значений температур на контактных поверхностях инструмента важная задача теплофизики резания. С этими законами связаны износ и стойкость режущих кромок и поверхностей лезвия, термические напряжения в инструменте, область режимов, при которых целесообразно использовать инструментальные материалы с той или иной степенью температурной устойчивости.

Под температурой резания понимается температура на контактных поверхностях инструмента при резании при установившемся теплообмене.

Для определения температуры резания необходимо знать количество теплоты, поступающей по зонам круглой пилы в процессе резания. Выделим две таких зоны (рисунок 1). Первая – режущая часть (зубья пилы), вторая – пильный диск (без зубьев).

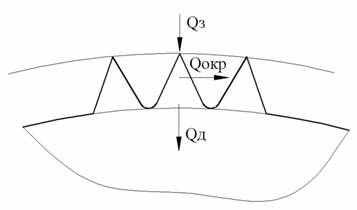
Рисунок 1 – Схема тепловых потоков по зонам круглой пилы

 

На рисунке 1 обозначено: QЗ – теплота, поступающая в инструмент через зубья, Вт; QД – теплота, поступающая в диск от режущей части, Вт; QОКР – теплота, передающаяся в окружающую среду от зубьев конвективной теплоотдачей, Вт.

Теплоотдачей излучением пренебрегаем, т.к. потеря тепла лезвиями зубьев от лучеиспускания не превышает, по данным работы [1], 1 – 1,5 % от общего количества тепла, поступающего в инструмент, и участвующего в теплообменных процессах с окружающей средой.

Распределение теплоты в процессе резания определяется уравнением теплового баланса. Для установившегося режима баланс теплоты для данного инструмента выглядит следующим образом

QЗ = QОКР + QД.                                                                    (1)

Теплота, поступающая в инструмент QЗ может быть определена из выражения

QЗ = Nрез К1,                                                             (2)

где       Nрез  – мощность резания, Вт;

К1 – коэффициент доли мощности на резание, идущей на нагрев инструмента, К1 = 0,025…0,35 [2].

Теплота, передающаяся в окружающую среду от зубьев конвективной теплоотдачей определяется по формуле

QОКР = z t0 aZ,                                                                      (3)

где       z – число зубьев пилы;

            t0 – температура резания, оС;

            aZ – среднеинтегральный коэффициент теплоотдачи зуба пилы, Вт/оС.

Среднеинтегральный коэффициент теплоотдачи зуба пилы aZ численно равен количеству теплоты, передаваемой зубом пилы в окружающую среду при повышении температуры резания на 1 оС в установившемся тепловом режиме, и может быть определен из выражения

,   (4)

где       b – толщина зуба (пильного диска), мм;

            b – угол заострения зуба, град.;

            aср – коэффициент теплоотдачи зуба в окружающую среду, Вт/(м2 оС);

b1 – вспомогательный угол, град.;

a – длина задней грани зуба, мм;

h – высота зуба в направлении биссектрисы угла заострения b, мм.

Теплота, поступающая в диск QД определяется из выражения [3]

,                                                                     (5)

где       ar – среднеинтегральный коэффициент теплоотдачи диска, Вт/оС;

DT – превышение температуры на периферии диска пилы (окружно­сти впадин зубьев) над окружающим воздухом, оС.

Среднеинтегральный коэффициент теплоотдачи диска ar может быть определен по формуле [3]

ar = 1,88×10-3×D0,96 V0,426 b0,471,                                               (6)

где       D – диаметр пилы, мм;

V – скорость резания, м/с.

Из выражений (1), (2), (3) и (5) получим формулу для определения температуры резания

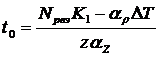.                                                    (7)

Для использования формулы (7) необходимо знать превышение температуры на периферии диска пилы над окружающим воздухом DT. Температурный перепад DT на периферии диска зависит от температуры резания t0 и может быть определен как

DT = К2×t0.                                                                 (8)

где       К2 – коэффициент, показывающий во сколько раз температура на периферии диска выше температуры резания, К2 = 0,025…0,1.

Тогда окончательная формула для определения температуры резания примет вид

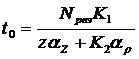.                                                          (9)

Рассмотрим определение температуры резания на конкретном примере: пиление круглой пилой (ГОСТ 980-80 тип 1, исполнение 1) диаметром D = 500 мм, толщиной b = 2,5 мм, число зубьев z = 60, частота вращения пилы n = 3000 мин-1, (скорость резания составит V = 78,5 м/с) коэффициент теплопроводности материала пилы l = 37,8 Вт/(м оС), коэффициент конвективной теплоотдачи a = 230 Вт/(м2 оС), скорость подачи u = 6 м/мин, высота пропила h = 50 мм, уширение зубчатого венца на сторону D = 0,75 мм, нижнее положение пилы, встречная подача, порода древесины – сосна.

Для данной пилы, согласно [4] шаг зубьев tз = 26,2 мм, высота зуба составит h » 0,5tз » 13 мм, длина задней грани зуба а » 0,4tз » 10,5 мм, угол заострения b = 40о, угол b1 » 165о. Радиус затупления лезвия принимаем r = 10 мкм.

Для данного режима резания мощность на резание, рассчитанная по методике [5] составит Nрез = 2300 Вт. Среднеинтегральный коэффициент теплоотдачи зуба пилы по формуле (4)

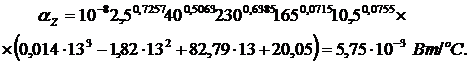
Среднеинтегральный коэффициент теплоотдачи диска по формуле (6)

ar = 1,88×10-3×5000,96 78,50,426 2,50,471 = 7,24 Вт/оС.

Следовательно, температура резания t0 для данного примера по формуле (9) составит

.

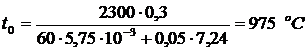Предложенная методика позволяет получить значения температур, ко­то­рые не противоречат известным данным. Методика может использоваться в ре­комендациях по выбору режимов работы инструмента, в которых в качестве ограничения его теплостойкость. Проводится экспериментальная проверка результатов теоретических исследований температурных полей зубьев круглых плоских пил.

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Конов В.Н. Исследование влияния тепловых явлений на работоспособность круглых пил: автореф. дисс. … канд. техн. наук: 13.00.01/ Конов Виктор Николаевич; ЛТА. – Л., 1979, – 26 с.

2. Щепочкин С.В. К вопросу о тепловых полях по зонам диска круглой пилы / С.В. Щепочкин // Социально-экономические и экологические проблемы лесного комплекса: Тез. докл. международ. науч.-техн. конф. / Урал. гос. лесотехн. ун-т – Екатеринбург, 2005. С.140.

3. Пашков В.К. Определение температурных перепадов плоских круглых пил [Электронный ресурс] / В.К. Пашков, С.В. Щепочкин // Материалы международной научно-технической Интернет конференции «ЛЕС-2006». – Режим доступа: http://science-bsea.narod.ru/les_2006/pashkov_opredelen.htm.

4. Библиографическое описание документа: ГОСТ 980-80. – Взамен ГОСТ 980-69; введ. 01.01.1982. – М., 1999. – 25 с.

5. Стахиев Ю.М. Руководящие технические материалы по определению режимов пиления древесины круглыми пилами / Стахиев Ю.М., Пашков В.К. – Архангельск: ЦНИИМОД, 1988. – 74 с.