Упругая деформативность поперек волокон с учетом анизотропии древесины

 

Глухих В.Н., (СПБГЛТА, г. Санкт-Петербург, РФ)

 

Упругая деформативность древесины характеризуется величиной обратной модулю упругости и изменяется в зависимости от угла наклона годичного слоя к пласти доски.

Для хвойных и лиственных пород анизотропия деформативности поперек волокон очень велика, но характер изменения упругих постоянных по сечению примерно одинаковый. Это проанализировано в работах Е.К. Ашкенази [1], [2], А.Н. Митинского [9], Н.Л. Леонтьева [7], С.Г. Лехницкого [8] и др. Использование полученных в работах [1], [8], [9] формул для вычисления постоянных упругости затруднено из-за применения ряда экспериментально определяемых величин, несовершенство методики исследования которых признают и сами авторы. К этим величинам относятся коэффициенты поперечной деформации, модули сдвига, модуль упругости .

Получение модуля упругости  теоретическим путем значительно упростило бы задачу исследования деформативности древесины поперек волокон.

Б.Н. Уголев [10] отмечает, что усушка древесины должна рассматриваться как результат деформирования некоторой ячеистой конструкции. При этом упругая анизотропия такой конструкции приобретает большое значение. Наибольшая усушка должна быть в направлении наименьшей жесткости системы и наоборот – наименьшая усушка будет иметь место в направлении наибольшей жесткости. Следовательно, если тангенциальная усушка больше радиальной, модули упругости по этим направлениям должны находиться в обратном соотношении. Это соотношение получено в работе [4] и предполагается, что оно справедливо не только для главных направлений анизотропии, но и для любых направлений поперек волокон:

Кr Еr = Кt Еt = Кx Еx                                                                                                   (1)

где Кr, Кt, Еr, Еt – коэффициенты усушки и модули упругости в главных направлениях анизотропии.

Учитывая известную формулу для коэффициента усушки [6]:

Кx = Кt sin2q + Кr cos2q,                                                                                              (2)

а также то обстоятельство, что при линейном деформировании древесины поперек волокон появляются угловая деформация, и наоборот, при сдвиге кроме угловой деформации появляется линейная [1], несложно получить:

                                                     (3)

Тогда из (1) можно записать:

                                                                                                             (4)

Из (4) с учетом (3) можно вычислить :

 = Еt                                                                                                                    (5)

Таким образом, при угле наклона годичного слоя 45° модуль упругости в направлении оси Х равен модулю упругости в тангенциальном направлении.

В формуле для модуля упругости [1], [8]

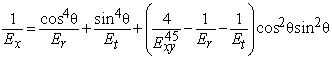
заменим из (5)  и получим:

,                                                              (6)

где a2 = Еt / Еr.

Таким образом, в формуле с коэффициентом Пуасссона и модулем сдвига [1], [8]

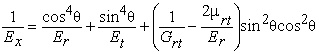
круглая скобка может быть заменена

 = , или                                                                                          (7)

Еt 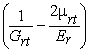 = 3 – a2.                                                                                          (8)

Точно такое же соотношение, как и в (8), получено при решении дифференциального уравнения [5], что лишний раз подтверждает правильность уравнений (1), (3).

Функция модуля упругости Ех из (6) приобретет экстремальные значения при q = 0, q = 90°, q = 60°. Причем, последнее значение есть минимум модуля упругости  (рис. 1):

                                                                                                        (9)

Для исследования деформативности пиломатериалов прямоугольных сечений удобнее использовать функцию (6) в декартовых координатах:

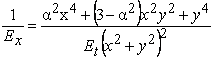                                                                            (10)

Анализируя результаты расчетов по формуле (10), можно видеть, что у досок с осью симметрии сечения, совпадающей с осью Y, наименьшая деформативность имеет место посередине пласти (рис. 2). От середины к краям пласти деформативность возрастает, достигает наибольшего значения и затем снижается, стремясь в пределе к обратной величине модуля упругости в радиальном направлении.


 

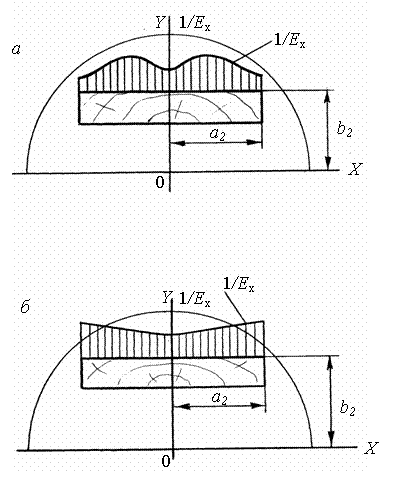
Рис. 2. Деформативность  по  ширине  пласти  досок:

а – промежуточного  расположения;  б – тангенциальных

 

Учитывая, что в точках посередине пласти возникают наибольшие напряжения (при сушке, при механических воздействиях в результате предотвращения поперечного коробления, при действии прижимных вальцов в станке на доски с поперечным короблением и т.д.), существует реальная опасность появления в этих местах трещин.


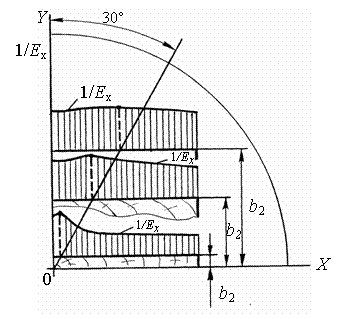
Деформативность радиальных досок по ширине пласти изменяется незаметно, исключая узкую локальную область, прилегающую к оси Y. По пласти тангенциальных досок деформативность также изменяется незаметно (рис. 3).

 

 

 

 

Рис. 3. Расположение  точки  максимума  на  кривой

деформативности  с  удалениями  доски  от  центра  бревна

 

По пласти полурадиальных досок деформативность изменяется от наименьших значений по краям до максимального в середине. Именно это, а также несколько более высокая прочность на растяжение в радиальном направлении по сравнению с тангенциальным, обеспечивает отсутствие пластевых трещин при высушивании.

Поэтому для пиломатериалов, предназначенных к высушиванию, необходимо при составлении плана раскроя бревен сделать так, чтобы наибольшая деформативность была в средней части пласти доски. Кривая деформативности должна быть обращена своей выпуклостью вверх.

Выводы:

1. При переходе от радиального направления к тангенциальному модуль упругости Ех принимает минимальное значение при угле наклона годичного кольца к пласти доски 30°.

При значении этого угла 45° модуль упругости Ех равен модулю упругости в тангенциальном направлении.

2. Изложенная методика определения наибольшей деформативности доски поперек волокон позволит проанализировать любую схему раскроя бревна по этому критерию.

3. Использование полученных результатов позволит планировать уже на стадии составления схемы раскроя бревна качество сушки пиломатериалов по остаточным напряжениям и пластевым трещинам.

 

 

 

Библиографический список

1. Ашкенази Е.К. Анизотропия древесины и древесных материалов. М.: Лесная промышленность, 1978. 223 с.

2. Ашкенази Е.К., Ганов Э.В. Анизотропия конструкционных материалов: Справочник. М.: Машиностроение, 1980. 247 с.

3. Глухих В.Н. Применение полиномов к решению задач для цилиндрически анизотропного тела // Технология и оборудование деревообрабатывающих производств: Межвуз. сб. науч. тр. СПб, ЛТА. 2001. С. 126-131.

4. Глухих В.Н. О возможной взаимосвязи постоянных упругости и коэффициентов усушки древесины // Технология и оборудование деревообрабатывающих производств: Межвуз. сб. науч. тр. СПб, ЛТА. 2002. С. 124-128.

5. Глухих В.Н. О соотношении постоянных упругости древесины как цилиндрически анизотропного тела // Технология и оборудование деревообрабатывающих производств: Межвуз. сб. науч. тр. СПб, ЛТА. 2003. С. 162-166.

6. Куликов Н.П. Усушка древесины в зависимости от направления относительно главных осей. Труды ЛТА, 1938. №51.

7. Леонтьев Н.Л. Упругие деформации древесины. М.-Л.: ГЛБИ, 1952. 117 с.

8. Лехницкий С.Г. Теория упругости анизотропного тела. М.: Наука, 1977. 415 с.

9. Митинский А.Н. Упругие постоянные древесины как ортотропного материала // Труды ЛТА им. С.М. Кирова / ЛТА. 1958. №63. С. 22-54.

10. Уголев Б.Н. Деформативность древесины и напряжения при сушке. М.: Лесная промышленность, 1977. С 174.