624.011.1 : 674.028 Левинский Ю.Б., Агафонова Р.И.

(УГЛТУ, г. Екатеринбург, РФ) levinskyi@bk.ru

Прогнозирование прочности древесины с учетом

геометрии строения древесины

Многие исследователи заметили, что прочность древесины меняется в зависимости от величины угла между направлением её волокон и вектором внешней нагрузки [1,2,3,4].

Это явление объясняется анизотропией древесного материала. Известно, что клетки, отвечающие за механическую прочность (трахеиды) также анизотропны.

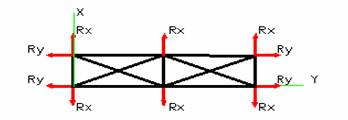
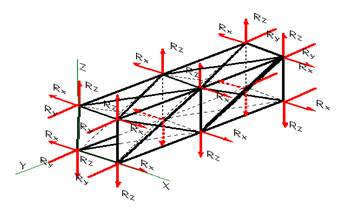
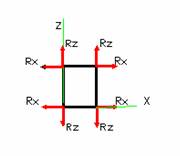
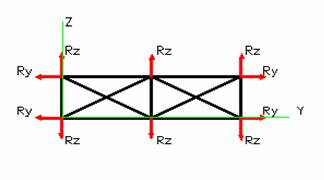
Авторами [1] была предложена схема стержневой системы, для теоретического определения и оценки напряженного состояния и прочности древесного материала. Заявленная схема является плоской, но при рассмотрении силовых взаимодействий, возникающих в деталях и конструкциях из древесины, представляется более обоснованным и корректным её объёмный (пространственный) аналог (рис. 1.).

Рис. 1. Схема расчетной стержневой системы для анизотропного тела

Используя предложенную методику расчета [1], и известные геометрические соотношения, произведем расчет напряжения, возникающего в древесине, при разных углах наклона вектора силового воздействия к направлению волокон.

Предельное сопротивление суммарного слоя (Z) с поперечной ориентацией микрофибрилл определяется по формуле:

Z= N₉₀/ (1+2cos³(90-γ)F_сп/F_h), ( 1)

где Z- предельное сопротивление суммарного слоя с поперечной

ориентацией микрофибрилл;

N₉₀ - предельное сопротивление разрыву поперек волокон;

λ – угол между приложенной нагрузкой и направлением

волокон;

γ – средний угол спиральных слоев для сосны

γ_ран= 30⁰, γ_позд= 17,3⁰;

F_сп,F_h – площади поперечного сечения соответственно, и

спиральных поперечных слоев.

Предельное сопротивление разрыву под углом λ≥ γ, под углом λ< γ и предельное состояние при чистом сдвиге вдоль волокон определяются соответственно по формулам 2-4:

σ _{р λ} ^пред =[ 1+0.25/(sin λ +tq γ cos λ)1.125] σ _{р 90} ^пред , (2)

σ _{р λ} ^пред =([ sin λ +0.25 cos(γ -λ)]/ [0.25 cos(γ -λ) (sin λ +tq γ cos λ)1.125])σ _{р 90} ^пред , (3)

σ _сдв^пред =2 F_сп σ _{р 90} ^пред / cos γ *1,125, (4)

Таблица 1

Расчетное предельное сопротивление древесины

при растяжении под углом к волокнам

Порода древесины	Значения показателя, МПа, при угле наклона волокон древесины, град.
	0	15	30	45	60	75	90
Сосна	9,02	9,9	11,73	9,45	8,50	8,83	8,78

Полученные расчетным методом величины предельных напряжений подтверждены экспериментально при испытании на прочность заготовок древесины сосны. Подбор и комплектование образцов по направленности распиловки позволил выявить зависимость прочностных показателей от угла встречи вектора силового воздействия и направлению волокон.

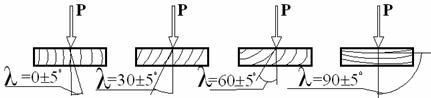
Рис. 2. Схема испытания образцов с учетом

ориентации волокон древесины

Для определения модуля упругости и напряжения при сжатии и растяжении под углом в 30, 45 и 60⁰ были сформированы группы образцов для каждого угла с допустимым изменением его величины в пределах ± 5⁰ .

Испытания показывают, что прочность древесины резко уменьшается с увеличением угла наклона волокон относительно вектора действующих внешних сил (табл.2, рис.3-5).

Таблица 2

Физико- механические показатели древесины сосны и осины

при растяжении и сжатии образцов с различной направленностью волокон

Угол встречи	Значения показателя для образцов из древесины
	Сосна				Осина
	Влажность,%	Предел прочности, МПа	Модуль упругости*		Влажность,%	Предел прочности, МПа	Модуль упругости*
			ГПа	%			ГПа	%
При растяжении
0	11,2	10,4	14,9	100	10,5	8,7	13,3	100
30	11,2	12,3	4,6	30,8	10,8	7,5	2,17	16,3
45	11,2	9,05	1,3	8,7	10	9,3	0,8	6
60	11,1	8,7	0,8	5,4	10,7	8,3	0,6	4,5
90	11,2	8,8	0,4	2,7	10,2	7,2	0,4	3
При сжатии
0	11,6	11,5	16,3	100	11,6	9,4	11,5	100
30	11,6	9,8	2,9	17,8	11,5	7,8	2,1	18,3
45	11,9	9,7	1,2	7,4	11,8	7,6	1,1	9,5
60	11,3	9,1	0,7	4,3	11,9	6,4	0,7	6
90	11,6	8,9	0,6	3,7	11,6	6,2	0,6	5,2

*величина модуля упругости относительно базовой характеристики, принимаемой для испытаний образцов вдоль волокон древесины. выраженная в процентах.

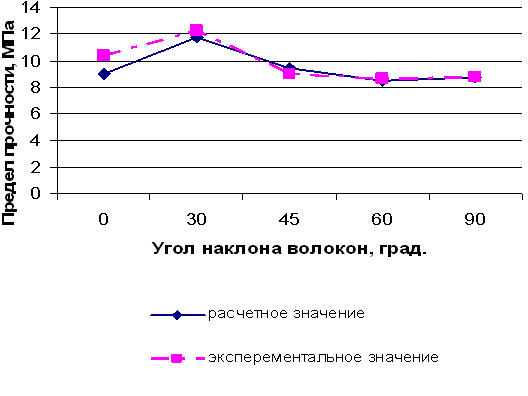
Рис.3. Зависимость предела прочности древесины

при растяжении от направления волокон

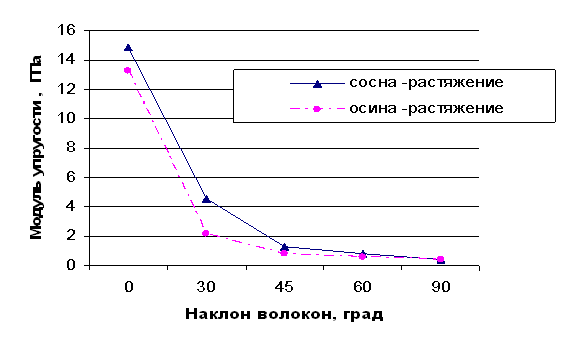
Рис.4. Зависимость модуля упругости при растяжении

от направления волокон

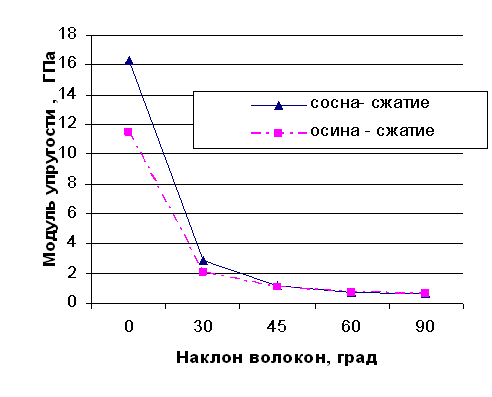
Рис.5. Зависимость модуля упругости при сжатии

от направления волокон

В результате проведенных экспериментально – теоретических исследований выявлено следующее:

1. Прочностные характеристики и, следовательно, конструкционные возможности древесины существенно зависят от её микростроения.

2. Механические показатели древесины, которые служат основой для расчета несущих конструкций, необходимо связывать с анатомическими особенностями древесины, учитывая при этом структуру материала по внешним, визуально определимым признакам.

3. Методы теоретического расчета напряжений в анизотропном материале, каковым является древесина, позволяют получить вполне достоверные значения напряжений, в том числе, и для комбинированных или сборно- клееных несущих конструкций.

4. Предельное напряжение разрыву достигает максимального значения при угле 30, что свидетельствует о равномерности напряженного состояния и сбалансированности деформаций во всех слоях и направлениях.

При проведении эксперимента в образцах с углом 30 град во время разрушения не замечено характерного потрескивания (показатель начала разрушения), а разрушение происходило резко и сопровождалось хлопком. Это ещё раз подтверждает теоретическое описание разрушения.

5. Модуль упругости древесины резко снижается, причем наиболее значительно его уменьшение происходит в диапазоне λ=0... 30⁰.

6. При проектировании конструкций необходимо учитывать полученные в исследовании данные, поскольку они позволяют наиболее рационально назначить состав пакета для склеивания в зависимости от структуры древесины и вида изделий.

7. Характер изменения модуля упругости остается практически одинаковым на всех этапах испытаний и не зависит от породы древесины (осина, сосна).

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Ю.В. Слицкоухов, В.Д. Буданов, М.М. Гаппоев и др. «Конструкции из дерева и пластмасс», под ред. Г.Г. Карлсена – М.: Стройиздат, 1986г.-543с.

2. Е.И. Савков «Прочность пиломатериалов»-Гослесбумиздат, 1962г.-85с.

3. А.М. Калугин «Деревянные конструкции», М. издат. АСВ, 2003г.-224с.

4. В.М. Хрулев «Долговечность клееной древесины», лесная промышленность, 1971г. -160с.