Новосёлов А.В. (УГЛТУ, г. Екатеринбург, РФ)

ЭЛЛИПТИЧНОСТЬ БРЕВЕН И ОПТИМАЛЬНЫЕ РАЗМЕРЫ ПИЛОМАТЕРИАЛОВ

Практически каждое бревно в поперечном сечении имеет отклонение от формы круга. У пиловочника хвойных пород полученного из нижней и средней части ствола, взаимно-перпендикулярные диаметры различаются на 3,1…3,7%. При среднем диаметре 30 см. эллиптичность возможна у 80% бревен [1]. Эллиптичность поперечного сечения бревна приводит к рассеиванию толщин и ширин пиломатериалов, что сказывается на спецификационном и объемном выходе пиломатериалов.

В [2] доказано что, теоретически из эллиптических бревен возможно получить пиломатериалы с таким же объемным выходом, что и из бревен круглого сечения. Рассматривая поперечное сечение бревна, с коэффициентом сбега равным единице, определялись оптимальные размеры пиломатериалов как оптимальные размеры прямоугольника вписанного в эллипс.

Данный пример рассмотрен для расчета относительно наибольшего (наименьшего) диаметра бревна (главных диаметров эллипса) перпендикулярно поставу, но не рассматривается случай определения оптимальных размеров под углом к поставу (при повороте эллипса).

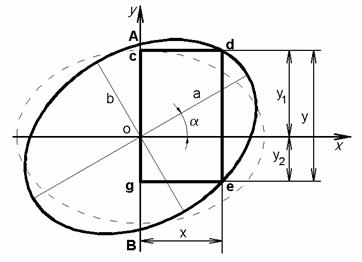
Решение данной задачи в общем виде, сводится к определению оптимальных размеров прямоугольника cdeg вписанного в половину эллипса ограниченного осью ABOY и дугой AdeB (рис. 1).

Рисунок 1 – Расчётная схема

При повороте эллипса относительно центра координат, формула эллипса примет вид:

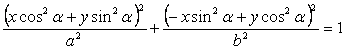, (1)

где α – угол поворота эллипса;

a, b – полуоси эллипса.

Решая уравнение (1) относительно y получим:

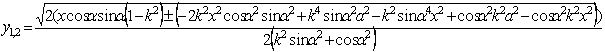(2)

где k – коэффициент сжатия эллипса , (k=b/a).

Площадь прямоугольника S_cdeg равна:

S_cdeg = ge · ed (3)

ed = |y₁|+|y₂| (4)

Тогда решая уравнение (4) с учетом уравнения (2) получим:

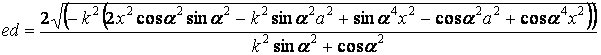(5)

Подставив значение уравнения (5) в уравнение (3) найдем площадь прямоугольника cdeg:

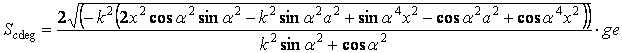(6)

Приравняв нулю производную от найденного выражения найдем оптимальное значение ge соответствующее максимальному значению площади прямоугольника:

(7)

решая уравнение (6) с учетом уравнения (7) найдем оптимальное значение ed соответствующее максимальному значению площади прямоугольника cdeg:

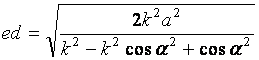(8)

В частном случае, при α=0, мы приходим к известным рекомендациям относительно оптимальных размеров при выработке одной пары досок: , .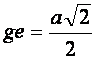

Полученные формулы могут быть использованы для определения размеров пиломатериалов выпиливаемых из эллиптичных бревен под углом к основным осям эллипса.

Библиографический список

1. Анучин, Н.П. Лесная таксация / Н.П. Анучин. –М.: Гослесбумиздат, 1960. – 521с.

2. Пижурин, А.А. Основы моделирования и оптимизации процессов деревообработки / А.А. Пижурин, М.С. Роземблит. -М.: Лесная промышленность, 1988. – 294с.