ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ ПАРАМЕТРОВ ПОРШНЯ

Раевская Л.Т.(УГЛТУ, г. Екатеринбург, РФ) raevskaya@usfeu/ru

PISTON TECHNOLOGICAL PARAMETERS OPTIMIZATION

Самым распространенным из семейства аксиально-поршневых реверсивных пневмомоторов является пневмомотор ДАР-14М, имеющий следующие технические характеристики: мощность – 10 кВт; частоту вращения (номинальное значение) – 400 об/мин; давление воздуха – 0.5 МПа; диаметр поршня – 82 мм. Поршень пневмомотора ДАР-14М литой, изготовлен из сплава АК7М2 (А – алюминий, К – кремний, 7%, М – медь, 2%). Литейные алюминиевые сплавы (ГОСТ 2685-75) обладают свойством жидко-текучести, имеют сравнительно небольшую усадку и используются в основном для фасонного литья. Нами в настоящей работе использовались следующие свойства вышеуказанного сплава: плотность ρ = 2.8 г/см ³ , модуль упругости 1 рода Е = =71000 МПа, коэффициент Пуассона ν = 0.31 [1].

Настойчивая деятельность проектировщиков, изготовителей, эксплуатационников в конце прошлого столетия позволила существенно повысить надежность и долговечность пневмомоторов, в том числе и ДАР-14М. Сейчас не наблюдаются такие отказы как распрессовка металлических или резиновых заглушек, скалывание кулачкового диска ротора, заклинивание поршней. Анализ оставшихся причин отказов пневмомоторов показал, что 80% отказов происходит из-за разрушения поршней, 12% - кулачкового диска ротора, 4% - пластмассовых заглушек цилиндров и т.д. Очевидно, что основное число отказов связано с поршнем.

Проведение конструктивных мероприятий для повышения надежности поршней пневмомоторов существенно упростилось за последнее десятилетие в связи с появлением инженерных программных комплексов таких, например, как ANSYS.

Математическое моделирование напряженно – деформированного состояния дает возможность разработки и внедрения, новых более точных методик расчета и оптимизации деталей пневмомоторов. Таким образом, исследования, направленные на разработку обоснованных методик расчета и проектирования, являются актуальной задачей. В настоящей работе мы ограничимся рассмотрением пневмомотора ДАР 14М, как наиболее востребованного в последнее время.

Постановка задачи

Из проведенных ранее исследований [2,3] следует, что возможно одной из причин разрушения поршня пневмомотора является то, что он испытывает кроме растяжения - сжатия еще и деформацию изгиба. Изменение положения деформированного поршня относительно недеформированного хорошо видно на рис.1 (особенно для точек левого торца поршня).

Рис.1.Деформированное и недеформированное состояния поршня.

Это приводит к нежелательному смещению точек торца поршня вдоль оси У, перпендикулярной к оси поршня Х. Кроме того, появляются значительно выше средних значения напряжения в области соединения ребра жесткости и опоры под поршневой палец (рис.2).

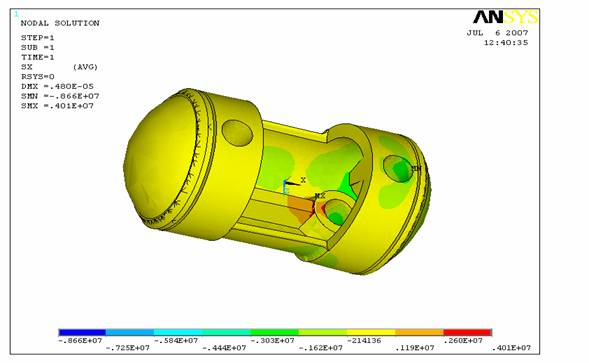
Рис.2. Напряжения вдоль оси поршня. В верхней части области соединения

ребра жесткости и опоры под поршневой палец появляются значительные растягивающие напряжения (0.401Е+07 Н/м²).

На рис.2 показано, что верхняя часть ребра жесткости растянута, в то время как нижняя – сжата. На рис.3 цветом отмечено смещение точек поршня относительно оси У при перемещении вдоль оси поршня. Максимальное смещение наблюдается у точек, расположенных на левом торце поршня. Это смещение достигает значения 0.437Е-05 м. Расчет поля напряжений, деформаций, смещений в теле поршня пневмомотора ДАР-14М произведен с помощью комплекса программ ANSYS относительно всех осей.

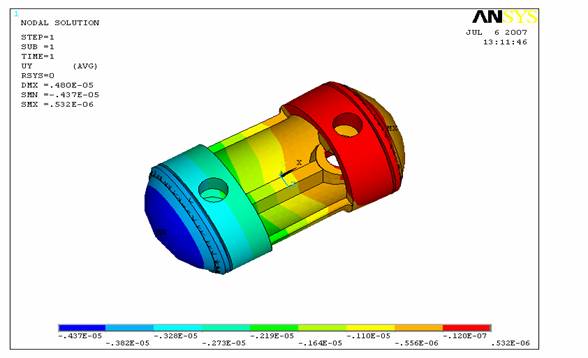
Рис.3. Смещение точек поршня вдоль оси У. Смещение нарастает при движении от правого торца поршня, где приложена нагрузка, к левому.

Причина появления деформации изгиба заключается в том, что линия действия равнодействующей внешних сил Р , которая совпадает с осью поршня, не совпадает с осью ребра жесткости. Эта линия смещена относительно оси ребра жесткости на расстояние Yо, оставаясь параллельной этой оси (рис.4). Возникает внецентренное растяжение – сжатие, что как известно приводит к появлению в сечениях ребра жесткости не только нормальный силы, но и изгибающего момента, равного М = Р*Yo. Плоскость действия момента – ХУ (см. рис.1), поэтому поворот сечений происходит вокруг оси Z. В этом случае добавка в нормальном напряжении, связанная с появлением изгибающего момента по нашим оценкам на порядок больше составляющей, связанной с нормальной силой. Очевидно, для уменьшения величины момента необходимо уменьшить плечо Уо (при постоянном значении силы Р). Это возможно, если изменить так форму сечения, чтобы его центр тяжести приблизить к оси поршня.

Задача расчета заключалась в исследовании влияния параметров ребра жесткости, в частности, параметров сечения на напряженно-деформированное состояние поршня. Цель такого исследования – определение таких параметров конструкции,

Рис.4. Ребро жесткости. Точка С – центр тяжести сечения. Х – ось ребра жесткости. Уо – координата точки приложения силы Р.

при которых смещения, напряжения и деформации становятся меньше, существующих в данном поршне в настоящее время. Так как проблема сложная, то для решения задачи привлекались численные методы.

Последовательность расчета

1. Геометрическая модель поршня была построена в программе ANSYS. При расчете использовалась конечно-элементная модель с упорядоченной сеткой конечных элементов, состоящей из 10-точечных тетраэдрических элементов (элемент SOLID92 в библиотеке конечных элементов ANSYS).

2. В программном файле ANSYS последовательно менялись параметры сечения – основания трапеции - а, в - и затем проводился расчет напряжений, деформаций и смещений при новых заданных параметрах. Набор выбранных для анализа параметров сечения приведен в таблице.

В поршне пневмомотора ДАР-14М ребро жесткости имеет длину 60 мм, сечение, перпендикулярное оси ребра, имеет геометрическую форму трапеции с верхним основанием а = 8 мм, нижним основанием в = 16 мм. Высота трапеции (рис.4)– 15 мм.

Таблица. Набор параметров сечения ребра жесткости.

Номер сечения	1	2	3	4	5	6	7	8	9
а (мм)	8	12	12	16	20	16	16	20	20
в (мм)	16	12	16	12	8	16	20	12	4

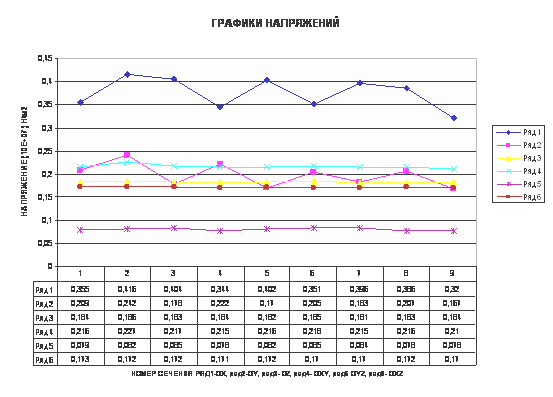
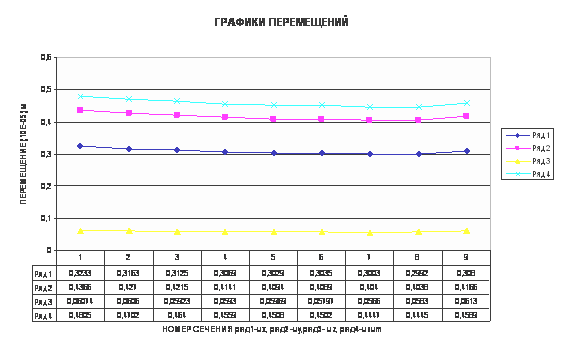
3. Результаты вычисленных значений напряжений, деформаций и смещений для разных сечений приведены ниже на графиках.

Ограничения.

1. Высота ребра жесткости не должна была превышать исходное значение. Это связано с движением кулачкового ротора, который не должен задевать ребро жесткости. Высота была выбрана постоянной для всех видов сечений и равной исходному значению h = 15 мм.

2. Для некоторых сечений масса ребра жесткости несколько возрастала. Этим увеличением пренебрегали в данном расчете.

3. Выбор параметров в качестве первого приближения делался с шагом 4 мм.

Результаты

1. Получены зависимости характеристик напряженно-деформированного состояния от параметров ребра жесткости.

2. Как следует из графически представленных результатов расчета, наименьшие напряжения по осям Х, У получены для сечения номер 9 с параметрами 20-4 (а-в); по оси Z и в плоскости ХУ - для сечения номер 7, с параметрами 16-20; в плоскости YZ - для сечений 4,8,9 с параметрами 16-12, 20-12 и 20-4; в плоскости XZ - для сечений 6,7,9 с параметрами 16-16, 16-20, 20-4. Таким образом, наиболее эффективными оказались сечения с номерами 9 и 7, а также 4, 6, 8.

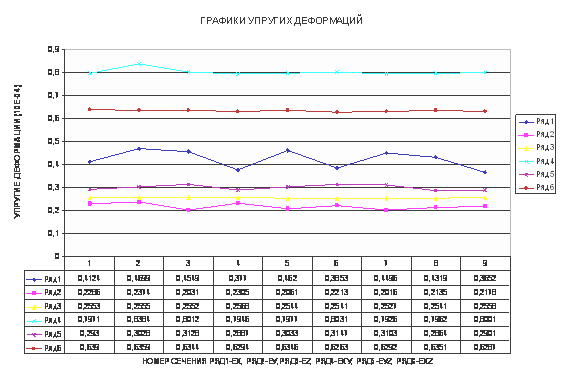
3. Упругие наименьшие деформации получены вдоль оси Х для сечения 9 с параметрами 20-4, относительно осей У, Z - для сечения номер 7 с параметрами 16-20, в плоскости ХУ - для сечения номер 7, в плоскости YZ – для сечения номер 8 с параметрами 20-12, наконец в плоскости ХZ- для сечения 6 с параметрами 16-16. Эффективными оказались сечения 9, 7, а также 6,8.

4. Наименьшие перемещения точек поршня получены следующие. Вдоль оси Х, У – для сечения 8 с параметрами 20-12, вдоль оси Z- для сечения номер 7 с параметрами 16-20, суммарное перемещение - для сечения номер 8 с параметрами 20-12. По параметру «смещение» более удачными оказались сечения 7, 8

5. Наименее удачный выбор - сечение номер 2 с параметрами 12-12, т.е. прямоугольное сечение. Практически все напряжения и упругие деформации оказались наибольшими. Хотя следует отметить, что смещения в этом случае оказались все-таки меньше смещений существующих у поршня пневмомотора ДАР-14М. У следующего прямоугольного сечения – сечения 6- характеристики лучше, чем у сечения 2.

6. У пяти сечений (номера 2,3,5,7,8) нормальное напряжение вдоль оси поршня – по оси Х - даже превышает наблюдаемое в поршне двигателя ДАР14М.

7. Из 9-ти сечений два сечения имеют прямоугольную форму (номера 2,6), три сечения (1,3,7) имеют форму трапеций с верхним основанием меньше по размеру нижнего, остальные сечения – в форме перевернутой трапеции. Сечения в виде перевернутой трапеции оказались самыми эффективными.

8. Сечения с номерами 2,9 не увеличивают массу поршня (их площадь равна площади существующего сечения, т.е. сечения под номером 1), что является предпочтительным.

Выводы. Рекомендации

1. Полученные результаты указывают на то, что существующее ребро жесткости в виде трапеции с параметрами а = 8 мм, в = 16мм у поршня пневмомотора ДАР-14М, не является оптимальным. Простой выбор нескольких других сечений привел в более предпочтительному напряженно-деформированному состоянию.

2. Хотя сечения в виде перевернутой трапеции оказались самыми эффективными, рекомендовать их следует с учетом следующего обстоятельства: учитывая то, что поршень – литой, необходимо выяснить, возможна ли отливка детали с такой формой сечения ребра жесткости.

3. Окончательный ответ на вопрос, какое сечение ребра жесткости наиболее эффективно, давать преждевременно. Следует исследовать и сечения с другими параметрами. При этом желательно сохранить массу равной исходной.

4. Поскольку самое большое напряжение вдоль оси поршня, то следует получить аналитическое выражение для этой величины и используя, например, метод неопределенных множителей Лагранжа, свести задачу оптимизации с ограничениями к задаче, решаемой методами исследования функций классического анализа [4].

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Гуляев А.П. Металловедение. Изд. Металлургия, М., 1966, 4-е издание, с.431

2. Раевская Л.Т. Математическое моделирование динамических процессов в аксиально-поршневых пневмомоторах. 1Х Всероссийский съезд по теоретической и прикладной механике. Аннотации докладов. Т. 111 (Нижний Новгород, 22-28 августа 2006). Нижний Новгород: Изд-во Нижегородского госуниверситета им. Н.И.Лобачевского, 2006. с.181-182.

3. Раевская Л.Т. Динамическое моделирование напряженно – деформированного состояния элементов аксиально-поршневых пневмомоторов. Деревообработка: технологии, оборудование, менеджмент ХХ1 века. Труды евразийского симпозиума/Под ред. И.Т. Глебова. – Екатеринбург. 2006 г. С.193-200.

4. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, том 1. М., 1966 г., 608 с.