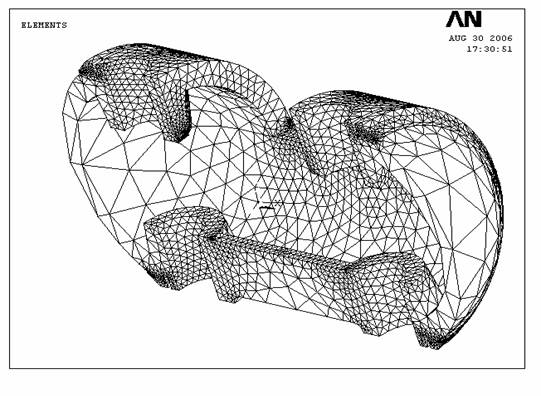
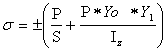Ранее было показано, что
параметры ребра жесткости не оптимальны [1]. Изменение параметров сечения ребра
жесткости может приводить к уменьшению характеристик напряженно-деформированного
состояния (НДС) от 4-5% (упругие деформации, абсолютные смещения точек) до 10-15% (напряжение). Для окончательного
решения задачи поиска формы и параметров сечения ребра жесткости исследуем целевую
функцию - в нашем случае нормальное напряжение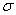 вдоль оси поршня. Воспользуемся методом неопределенных
множителей Лагранжа, который особенно эффективен при числе переменных три и
менее [2]. В данном расчете целевая функция зависит от двух параметров – размеров верхнего и нижнего оснований
трапеции. Эти параметры выбраны в качестве переменных проектирования. Кроме
того, потребуем, чтобы масса ребра жесткости оставалась постоянной, равной исходной
массе в поршне пневмомотора ДАР-14М. Это налагает ограничения
на переменные проектирования: поскольку площадь сечения должна оставаться
постоянной, равной S = h (а
+ b)/2, то отсюда
следует, что ограничение в виде равенства имеет следующий вид (а + b – k) = 0. В полученном условии
связи значение k равно
24. Изменяя переменные проектирования, можно влиять на переменные состояния –
напряжения. Чтобы построить функцию
Лагранжа
вдоль оси поршня. Воспользуемся методом неопределенных
множителей Лагранжа, который особенно эффективен при числе переменных три и
менее [2]. В данном расчете целевая функция зависит от двух параметров – размеров верхнего и нижнего оснований
трапеции. Эти параметры выбраны в качестве переменных проектирования. Кроме
того, потребуем, чтобы масса ребра жесткости оставалась постоянной, равной исходной
массе в поршне пневмомотора ДАР-14М. Это налагает ограничения
на переменные проектирования: поскольку площадь сечения должна оставаться
постоянной, равной S = h (а
+ b)/2, то отсюда
следует, что ограничение в виде равенства имеет следующий вид (а + b – k) = 0. В полученном условии
связи значение k равно
24. Изменяя переменные проектирования, можно влиять на переменные состояния –
напряжения. Чтобы построить функцию
Лагранжа
L (X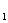 , X
, X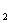 ,
, 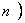 =
= 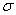 ( X
( X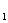 , X
, X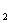 ) +
) +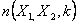
 , (1)
, (1)
где  - неопределенный множитель Лагранжа, X
- неопределенный множитель Лагранжа, X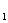 , X
, X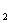 - параметры, необходимо получить аналитическое
выражение для напряжения в сечении ребра жесткости. Известно, что напряжение
вычисляется по формуле
- параметры, необходимо получить аналитическое
выражение для напряжения в сечении ребра жесткости. Известно, что напряжение
вычисляется по формуле
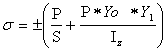 . (2)
. (2)
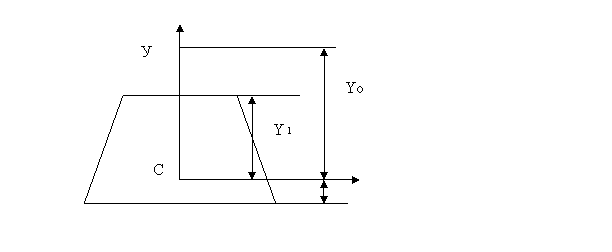
Рис.2. Сечение ребра жесткости. Ус – расстояние от нижнего
основания трапеции до центра тяжести сечения - т. С, У - координата самой удаленной точки сечения от нейтральной
линии, Уо – координата точки приложения силы Р.
- координата самой удаленной точки сечения от нейтральной
линии, Уо – координата точки приложения силы Р.
Здесь Р – равнодействующая внешних
сил, направленная по оси поршня, перпендикулярно
плоскости рис.2 на расстоянии Уо от точки С, 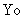 - плечо силы Р относительно оси Z,
- плечо силы Р относительно оси Z, 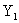 - координата самой удаленной от нейтральной линии точки
сечения,
- координата самой удаленной от нейтральной линии точки
сечения, 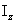 - момент инерции сечения
относительно оси Z. В
данном расчете величина силы Р считается постоянной, а
Ус, У
- момент инерции сечения
относительно оси Z. В
данном расчете величина силы Р считается постоянной, а
Ус, У , Уо, I
, Уо, I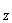 зависят от параметров a,b следующим образом:
зависят от параметров a,b следующим образом:
Ус = h ( 2a + b)/3(a + b) ;
У = h – Ус = h(a + 2b)/3(a + b) ; (3)
= h – Ус = h(a + 2b)/3(a + b) ; (3)
Уо = d – Ус = (3d (a +b ) – h(2a
+ b))/3(a + b) ; (4)
I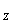 = h3 (a2 + 4ab + b2)/36(a + b), (5)
= h3 (a2 + 4ab + b2)/36(a + b), (5)
где d
– расстояние от нижнего основания трапеции до оси поршня. Эта величина для двигателя
ДАР -14М принимает значение равное 32,5 мм. Подставляя соотношения (3) – (5)
в формулу (2), получаем для максимального нормального
напряжения вдоль оси поршня в самой удаленной от нейтральной линии точке сечения
аналитическое выражение в виде
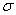 =
= 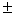
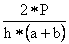 {1 + 2(a + 2b)[3d(a +
b) – h(2a + b)] /h(a2 + 4ab + b2)}. (6)
{1 + 2(a + 2b)[3d(a +
b) – h(2a + b)] /h(a2 + 4ab + b2)}. (6)
В силу симметрии задачи нейтральная линия пройдет
параллельно основаниям трапеции Определим координату У
нейтральной линии из соотношения (2). Получаем
У = - 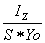 , откуда следует, что для У всегда
будет отрицательное значение, т.е. нейтральная линия располагается всегда ниже
центра тяжести сечения. Часть ребра жесткости над центром тяжести всегда –
сжата, независимо от вида трапеции. Возникает вопрос, при любых ли параметрах a,b сечения точки
именно верхнего основания будут самыми удаленными от нейтральной линии. При
величине a
, откуда следует, что для У всегда
будет отрицательное значение, т.е. нейтральная линия располагается всегда ниже
центра тяжести сечения. Часть ребра жесткости над центром тяжести всегда –
сжата, независимо от вида трапеции. Возникает вопрос, при любых ли параметрах a,b сечения точки
именно верхнего основания будут самыми удаленными от нейтральной линии. При
величине a 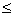 b это так и будет. При значениях
b это так и будет. При значениях
а  16 мм самыми удаленными точками от нейтральной линии
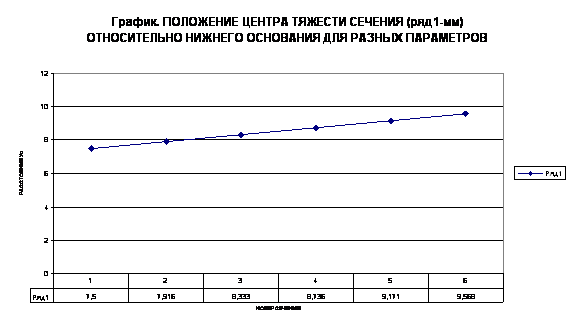
оказываются точки нижнего основания. Ниже на графике показано изменение
расстояния (в мм) до центра тяжести для нескольких вариантов сечений: 1 –
сечение с параметрами а=b=12; 2- a=14, b=10; 3 – a=16,
b=8; 4 – a=18, b=8; 5 – a=20, b=4; 6 – a=22,
b=2. Для нашего
исследования рассмотрим напряжение в
виде соотношения (6).
16 мм самыми удаленными точками от нейтральной линии
оказываются точки нижнего основания. Ниже на графике показано изменение
расстояния (в мм) до центра тяжести для нескольких вариантов сечений: 1 –
сечение с параметрами а=b=12; 2- a=14, b=10; 3 – a=16,
b=8; 4 – a=18, b=8; 5 – a=20, b=4; 6 – a=22,
b=2. Для нашего
исследования рассмотрим напряжение в
виде соотношения (6).
Функция Лагранжа получается следующей (при условии h=15, d=32,5)
L(a, b, n)= 2P(1+ 2(2b+a)(67.5a+82.5b)/15(a2+4ab+b2))/15(a+b) + n(a+b-k). (7)
Для частных производных от функции Лагранжа (7) по а, b, n получены следующие выражения
∂ L
(a, b, n) /∂ a = (0.07(15na4 + 120nba3 – 20a2P
+ 270 a2nb2 – 92aPb + 120 anb3 – 164Pb2+
15nb4))/(a2+ 4ab + b2)2
∂ L
(a, b, n) /∂ b = (0.07(15na4 + 120nba3 – 34a2P
+ 270 a2nb2 – 40aPb + 120 anb3 – 46Pb2+
15nb4))/(a2+ 4ab + b2)2
∂ L
(a, b, n) /∂ n
= a + b – k.
Приравнивая эти производные нулю и решая систему уравнений,
получаем для параметров а и b, минимизирующих нормальное наибольшее напряжение значения
(округляя до целых величин) а = 20
мм, b=4
мм.
Обсуждение результатов.
- Поскольку самое большое напряжение
существует по оси поршня, то получено аналитическое выражение для этой
величины и с помощью метода неопределенных множителей Лагранжа, вычислены
такие параметры а, b
сечения ребра жесткости, которые минимизируют нормальное наибольшее напряжение.
- Для проверки результата в программном комплексе ANSYS исследовалось напряженно-деформированное
состояние поршня пневмомотора ДАР-14М с новыми параметрами
ребра жесткости а=20, b=4. В таблице приведены некоторые
результаты для максимального смещения
Uy,
напряжений
 ,
, 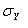 деформации
деформации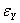 в сравнении с полученными ранее ( предыдущего расчета поршня с параметрами а=8 мм, b=16 мм).
в сравнении с полученными ранее ( предыдущего расчета поршня с параметрами а=8 мм, b=16 мм).
Таблица
1.
Характеристики
напряженно-деформированного состояния (НДС) для двух видов
сечения
ребра жесткости
|
a-b (мм)
характе-
ристики
|
8- 16
|
20-4
|
% изменения
|
|
Uy (10Е-05)м
|
-0.437
|
-0.416
|
4.8
|
|
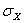 (10Е07) Н/м2 (10Е07) Н/м2
|
0.356
|
0.320
|
10.1
|
|
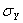 (10Е07) Н/м2 (10Е07) Н/м2
|
0.209
|
0.167
|
20.1
|
|
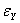 (10Е-04) (10Е-04)
|
0.229
|
0.217
|
5.2
|
Для дальнейшего уточнения результатов
необходимо рассмотреть сечение ребра жесткости вместе с корпусом поршня.
Библиографический список
- Раевская Л.Т. Динамическое моделирование напряженно
– деформированного состояния элементов аксиально-поршневых пневмомоторов. Деревообработка: технологии,
оборудование, менеджмент ХХ1 века. Труды
евразийского симпозиума/ Под ред. И.Т. Глебова. –
Екатеринбург. 2006 г.
С.193-200.
- Петрушко И.М., Кузнецов
Л.А., Прохоренко В.И., Сафонов В.Ф. курс высшей
математики: Интегральное исчисление. Функции нескольких переменных. Дифференциальные
уравнения. М.: Изд-во МЭИ, 2002.