ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ДЛЯ ПРОГНОЗИРОВАНИЯ СЛОЖНЫХ РИСУНКОВ НА ПОВЕРХНОСТИ КЛЕЕНЫХ ИЗ ШПОНА ДЕКОРАТИВНЫХ ЭЛЕМЕНТОВ МЕБЕЛИ И СТОЛЯРНО–СТРОИТЕЛЬНЫХ ИЗДЕЛИЙ.         

 

Игнатович Л.В., Шишов А.В., Осоко С.А. (БГТУ, г.Минск, РБ) andruha26@yandex.ru

 

Application of mathematical modelling for forecasting of difficult drawings for surfaces agglutinate from veneer sheets of decorative elements of furniture and stoljarno-building products.

 

Разработка импортозамещающей технологии позволяющей создавать декоративные изделия с абсолютным эффектом натуральной древесины, поможет подчеркнуть особенности изделий мебели и интерьера, позволит обеспечить мебельные предприятия сравнительно не дорогим облицовочным материалом на основе лущеного шпона из малоценных пород древесины, имитирующим текстуру ценных пород древесины.

Следовательно, первоочередная задача для создания сложных, фигурных рисунков и текстур древесины на поверхности декоративных элементов заключается в прогнозировании рисунка в сечении клееного блока, после серии механических преобразований пакета шпона. В связи с этим необходимо использовать методы математического моделирования для получения необходимого рисунка на поверхности клееных из шпона декоративных элементов мебели.

Для нахождения состава пакета позволяющего получить декоративный элемент с заданным рисунком можно использовать различные методы решения. Самым простым является метод полного перебора возможных вариантов. Суть метода состоит в том, что на каждом шаге итерации один из листов шпона в пакете поворачивается на некоторый угол и пакет подвергается операции изгиба на произвольной пространственной фигуре. В качестве пространственных фигур можно использовать как простейшие, такие как цилиндр, шар, так и более сложные получаемые использованием тригонометрических функций по отдельности и совместно.

После этого проводится анализ полученного рисунка на различных срезах. В случае если полученный рисунок не соответствует заданному необходимо повторить операцию по модификации пакета шпона. При этом количество вариантов, которые необходимо рассмотреть для получения решения определим по формуле [1]:

                                                         

где S – количество слоев шпона в пакете, шт; Δα – минимальный угол поворота листа шпона в пакете; M – количество функций модификации формы пакета шпона; D – количество функций применяемых к пакету единовременно.

При S = 100 и Δα = 1° MD = 8 N ≈ 3,414 10256. Такое количество вариантов не может быть решено за разумный промежуток времени.

Поэтому для решения данной задачи предлагается применить генетические алгоритмы, которые являются наиболее предпочтительными методами многоэкстремальной оптимизации. Генетические алгоритмы – адаптивные методы поиска, которые в последнее время часто используются для решения задач функциональной оптимизации. Они основываются на идее эволюции с помощью естественного отбора и по принципу «выживает наиболее приспособленный», чем выше приспособленность особи, тем выше вероятность того, что у потомков, полученных с её участием, признаки, определяющие приспособленность, будут выражены ещё сильнее, открытому Чарльзом Дарвином [2].

Если принять, что каждая особь популяции является точкой в координатном пространстве оптимизаци­онной задачи , а приспособленность особи соответствующим значением функции цели f(X), то популяцию особей можно рассматривать как множество координатных точек в пространстве, а процесс эво­люции – как движение этих точек в сторону оптимальных значений целевой функции.

 Следует отметить, что классический генетический алгоритм находит глобальный экстремум в вероятностном смысле. И эта вероятность зависит от числа особей в популяции. Как показали исследования, при оптимизации сложных многоконтурных и многосвязных систем регулирования и аналогичных систем с нейроконтроллерами генетические алгоритмы (в частности диплоидная версия ГА) с достаточно высокой вероятностью находят глобальный экстремум. Однако вычисление функции цели отдельных видов зачастую требует значительных вычислительных ресурсов, что существенно сказывается на общем времени работы ГА.

В отличие от существующих градиентных и численных алгоритмов, например, метода деформируемого многогранника Нелдера-Мида [3], генетический алгоритм начинает работу с некоторого случайного набора исходных решений, который называется популяцией. Каждый элемент из популяции называется хромосомой и представляет собой некоторое решение проблемы в первом приближении. Хромосома состоит из генов. Каждый ген является частью решения. Хромосомы изменяются (эволюционируют) на протяжении множества итераций, носящих название поколений (или генераций). В ходе каждой итерации хромосома оценивается с использованием некоторой меры соответствия – функции соответствия. Для создания следующего поколения новые хромосомы, называемые отпрысками, формируются путем скрещивания двух хромосом – родителей из текущей популяции либо путем случайного изменения (мутации) одной хромосомы. Новая популяция формируется, во-первых, путем выбора согласно функции соответствия некоторых родителей и отпрысков и, во-вторых, путем удаления оставшихся для того, чтобы сохранять постоянным размер популяции.

Существует два главных преимущества генетических алгоритмов перед классическими оптимизационными методиками.

1. Генетический алгоритм не имеет значительных математических требований к видам целевых функций и ограничений. Исследователь не должен упрощать модель объекта, теряя ее адекватность и искусственно добиваясь возможности применения доступных математических методов. При этом могут использоваться самые разнообразные целевые функции и виды ограничений (линейные и нелинейные), определенные на дискретных, непрерывных и смешанных универсальных множествах.

2. При использовании классических пошаговых методик глобальный оптимум может быть найден только в том случае, когда проблема обладает свойством выпуклости. В то же время эволюционные операции генетических алгоритмов позволяют эффективно отыскивать глобальный оптимум [4].

Для формирования хромосом создаем гены, соответствующие углу поворота листа шпона. Для описания генов используем бинарную запись.

Так как угол поворота не может составлять больше 360° для записи гена используем 9 битов, что позволяет закодировать 512 углов поворота, пример кодирования углов поворота представлен в ниже приведенной таблице.

 

 

 

 

Таблица – Кодирование угла поворота

Номер типоразмера

Угол поворота

Ген

1

0

000000000

2

1

000000001

3

2

000000010

4

3

000000011

…

…

…

361

360

100110100

На основании полученных генов формируются хромосомы, которые представляют собой наборы генов. При составлении хромосомы необходимо учитывать количество входящих в нее генов. В нашем случае количество генов равно количеству слоев шпона в пакете. Хромосома будет иметь вид

100001011011011100001011011011100001011….

Формирование хромосом осуществляется путем использования датчика псевдослучайных чисел [5].  Каждое число представляет собой номер угла поворота, соответствующий ген которого записывается в хромосому.

Количество хромосом, входящих в популяцию, принимается не менее 10.

Над выбранными хромосомами проводится операция скрещивания. При выполнении этой операции осуществляется обмен частями хромосом между двумя (может быть и больше) хромосомами в популяции. Обмен осуществляется следующим образом. С помощью датчика псевдослучайных чисел выбирается одна из возможных точек разрыва хромосомы. Точка разрыва – участок между соседними битами в строке. Обе родительские хромосомы разрываются на две части по этой точке. Затем соответствующие участки различных родителей склеиваются и получаются две хромосомы потомков. Одноточечный оператор скрещивания (точка разрыва равна 16):

До скрещивания

После скрещивания

1000010110110111 00001011011011100001011

1000010110110111 11000010111000010110110

1110000101101101 11000010111000010110110

1110000101101101 00001011011011100001011

Полученные новые хромосомы популяции подвергаются операции мутации – стохастическому изменению части гена. Приняв значение коэффициента вероятности мутации pмут = 0,01, подвергнем в среднем 1% всех битов популяции мутации. Каждый бит имеет одинаковый шанс подвергнуться мутации. С помощью датчика псевдослучайных чисел выбираются номера битов, которые будут подвергнуты мутации. Значения этих битов будут заменены на противоположные:

Оператор мутации (мутировал 20 бит):

До мутации

После мутации

1000010110110111110        0 0010111000010110110

1000010110110111110         1 0010111000010110110

Работа генетического алгоритма представляет собой итерационный процесс (рис. 4.2), который продолжается до тех пор, пока не выполняется заданное число поколений или пока не будет получен рисунок на поверхности декоративного отделочного материала, отличающийся от заданного на заранее оговоренную величину.

ga4

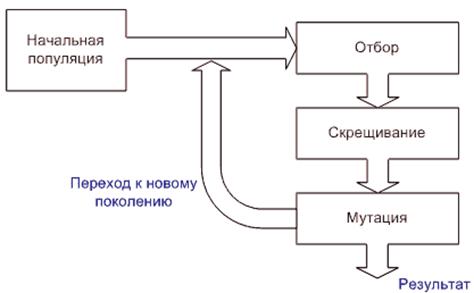
Рисунок - Алгоритм работы генетического алгоритма

Таким образом, используя методы математического моделирования, в частности применение метода генетических алгоритмов позволит прогнозировать рисунки на поверхности декоративного облицовочного материала полученного из шпона мягких лиственных пород древесины, имитирующие текстуру ценных пород древесины.

 

 

Библиографический список.

1. Писаревский А.Н. и др. Системы технического зрения (принципиальные основы, аппаратное и математическое обеспечение). – Л.: Машиностроение. Ленингр. отделениение, 1988 – 424 с.

2. Чарльз Дарвин. Происхождение видов.

3. Nelder J.A.,Mead R., A Simplex Method For Function Minimization, Computer J., No 7, 1964 P. 308-313.

4. John Holland, "Adaptation in Natural and Artifical Systems", 1975

5. Ротштейн А. П. Интеллектуальные технологии идентификации.