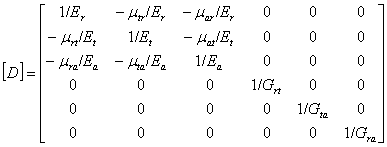Моделирование физико-механических свойств древесины при
конечно-элементном анализе столярных изделий
Пардаев А.С. (БГТУ, г. Минск, Республика Беларусь) pas6126020@mail.ru
Methodical principles of modelling of physicomechanical properties
of wood
are stated at the
analysis of the is intense-deformed condition of joiner's designs on the basis Finite
Element Method
Введение.
К столярным относятся изделия, изготавливаемые полностью или в основном из
древесины и древесных материалов: несущие, ограждающие конструкции и элементы зданий
(например, окна, двери, перегородки, щиты и панели, покрытия пола), мебель,
корпуса теле- и радиоаппаратуры, музыкальные инструменты и многое другое [1].
Они характеризуются тщательной обработкой поверхности, точной пригонкой
соединений и сборочных единиц.
Производство столярных изделий является крупным
потребителем древесины и характеризуется большими объемами производства.
Активизация жилищного строительства требует поставки большого количества
столярно-строительных изделий, отвечающих все возрастающим эксплуатационным
требованиям.
Прочность, надежность и
долговечность столярных изделий (СИ) в значительной мере зависит от правильного
выбора размеров деталей, элементов, их соединений и применения соответствующих
материалов.
В настоящее время наряду с традиционными способами оценки
прочности изделий все чаще используются подходы, основанные на численных
методах. Это связано с внедрением систем автоматизированного проектирования,
усложнением геометрии и структуры конструкций с ужесточением требований к их
прочности, а также сокращением сроков, отводимых на подготовку производства продукции.
Существует несколько математических методов реализации
представления геометрии в системах анализа, основанных на численных методах,
это:
·
метод конечных
разностей (МКР);
·
метод конечных
элементов (МКЭ);
·
метод граничных
элементов (МГЭ)
МГЭ является весьма перспективным, но пока еще не нашел практического
применения.
С помощью МКР реализованы многие системы анализа линейного
программирования (MAGMASOFT, AFS, CastCAE, LVMFlow и др.). Это вызвано
простотой применения данного метода, хотя он имеет существенный недостаток,
заключающийся в искажении геометрии при ее ступенчатом представлении (например,
периметр круга, представленного МКР, равен периметру описанного вокруг него
квадрата).
МКЭ [2] позволяет описать геометрию с любой степенью
точности, поэтому его применение представляется более предпочтительным. Следовательно,
для повышения точности моделирования следует выбирать систему, основанную на МКЭ.
В большинстве современных программных комплексов (например, ANSYS, NASTRAN,
ABAQUS, ProCAST, SIMTEC, PASSAGE/PowerCAST, ПОЛИГОН) численный анализ
реализован с помощью МКЭ.
Использование систем конечно-элементного анализа делает
возможным исследование объектов без изготовления их материального прототипа,
путем создания и решения адекватной математической модели. Это позволяет в
несколько раз сократить период конструкторско-технологической подготовки
производства продукции, материальные расходы и оптимизировать конструкцию по
определенным критериям.
Однако, применение метода конечных элементов, при анализе
столярных конструкций, требует больших знаний о самом методе, опыта работы и наличие
прикладных методик расчета СИ, учитывающих особенности древесного материала и
действительной работы конструкций.
Цель проведенного исследования – повышение
эффективности конструкционного анализа столярных изделий на основе численных
методов расчета напряженно-деформированного состояния за счет снижения затрат в
процессе подготовки производства на стадиях разработки изделий.
В соответствии с указанной целью сформулированы основные
задачи исследования:
·
предложить модель
физико-механических свойств древесины при
конечно-элементном анализе СИ;
·
разработать прикладную
методику расчета СИ, которая позволит учесть особенности физико-механических
характеристик древесного материала (анизотропию, усушку и разбухание);
Рассмотрим методику моделирования и результат
решения задачи прогнозирования напряженно-деформированного состояния СИ на
примере столярной плиты, состоящей из склеенных между собой сосновых реек, которое
возникает вследствие внешних воздействий (набухание древесины вследствие ее увлажнения). Воспользоваться при этом можно различными компьютерными системами
конечно-элементного анализа, например ANSYS, позволяющей учесть анизотропию
физико-механических свойств древесины, а также их
изменчивость при изменении влажности древесины.
В процессе моделирования свойств древесины
и анализа столярных конструкций приняты следующие допущения:
1.
У
древесины близкая к линейной зависимость между напряжением и деформациями
наблюдается при кратковременных нагрузках до величины напряжений,
соответствующих пределу пропорциональности. При этом можно с некоторым приближением считать, что
древесина подчиняется закону Гука. Структурные особенности древесины определяют
явно выраженные различия упругих свойств по разным направлениям, т.е. упругую
анизотропию [3]. Следовательно, применительно к древесине, связь между напряжениями
и деформациями осуществляется через упругие постоянные на базе теории упругости
анизотропного тела.
Основное соотношение между напряжением и деформацией для
упругих анизотропных материалов, в том числе и древесины, в матричной форме имеет
вид:
(1)
где 
- вектор деформаций; 
- матрица податливости; 
- вектор напряжений; 
– вектор начальных деформаций,
в данной модели предлагается рассматривать как вектор влажностных деформаций.
Матрица податливости для анизотропных материалов, размером
6´6, имеет вид:
где E – модуль упругости, G – модуль сдвига, μ – коэффициент поперечной деформации. При этом в соответствии
с ГОСТ 16483.29-73 [4] и ГОСТ 16483.30-73 [5], первый индекс μ указывает направление поперечной
деформации e, второй – направление вызвавшего ее напряжения σ. Двойные индексы G соответствуют направлениям осей
симметрии, между которыми происходит изменение прямого угла. Индекс 
указывает направление
вдоль волокон древесины, 
– радиальное направление поперек волокон, 
– тангенциальное направление поперек волокон.
Исходя из допущения о существовании
упругого потенциала (3)
; 
; 
(3)
и
ограниченных возможностей существующего, в настоящее время, программного
обеспечения, имеет смысл преобразовать матрицу податливости к симметричному виду,
путем усреднения попарно равных величин записанных в соотношениях (3).
Например, для сосны, с учетом
справочных данных [6] и экспериментальных [3], матрица податливости (2)
имеет вид, Па:
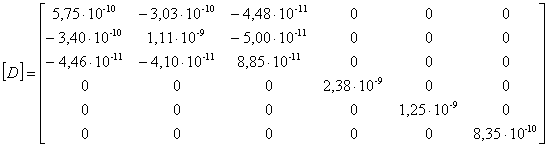(4)
Усредненная и симметричная, принятая в дальнейших расчетах,
матрица податливости для сосны имеет вид, Па:
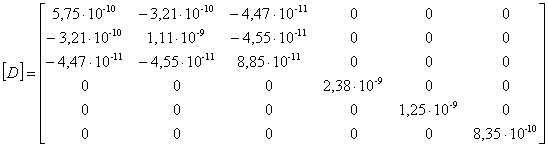(5)
Сравнивая исходную (4) и преобразованную матрицу
податливости (5) можно отметить их незначительное отличие, а стало быть, и
правомерность использования симметричной матрицы.
Вектор влажностных деформаций в матричной форме имеет
вид:
где W – влажность
древесины в начальный момент времени; W
– конечная влажность древесины; 
, 
, 
– коэффициент усушки/разбухания в радиальном,
тангенциальном и продольном направлении соответственно. Значения указанных
коэффициентов приняты в соответствии с экспериментальными данными [3].
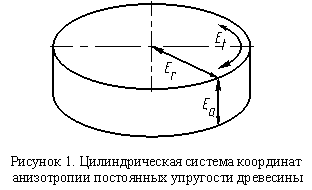
2.
Все параметры,
характеризующие физико-механические свойства древесины, заданы с учетом цилиндрической
системы координат (рис. 1).
3.
Для учета изменения механических
свойств древесины при изменении ее влажности, использованы
соотношения для пересчета к нормализованной влажности в соответствии с ГОСТ 16483.24-73
– ГОСТ 16483.30-73 [4, 5].
4.
Все нагрузки являются
установившимися во времени.
Описание
конструкции. Клееный щит состоит из пяти реек
древесины сосны сечением 44´110 мм, соединенных между собой по длине. Схема
расположения годичных слоев в смежных рейках принята случайным образом.
Расчетное увеличение влажности древесины составляет 22%, что соответствует изменению
начальной влажности образца от 8% до предела насыщения клеточных стенок.
Описание методики
эксперимента. Клееный щит в течении 7 часов находятся в камере при температуре 70° и
относительной влажности воздуха 100%. Далее 14 часов выдержка при температуре
20° и относительной влажности воздуха 100% для выравнивания влажности по
сечению бруска. После чего, снова образцы находятся в камере при температуре
70° и относительной влажности воздуха 100%. Периодически осуществляется контроль влажности образцов и
их масса. По достижении влажности более 30% и массы образцов более
расчетной образцы извлекают. Образцы укладывают на лист бумаги и обводом
по контуру отмечают профиль. Максимальный прогиб замерялся с помощью цифрового штангенциркуля
ГОСТ 166-80. Масса брусков определялась с помощью электронных весов SCOUT
6000x1.
Методика моделирования нагрузок и воздействий при решении
статических задач с использованием систем конечно-элементного анализа представлена
в литературе [7], а на примере столярных конструкций в работе [8].
Основные результаты натурного эксперимента и конечно-элементного
моделирования столярной плиты представлены на рис. 2–5. На рис. 2. представлен
внешний вид образца после окончания натурного эксперимента с указанием
максимального прогиба равного
Рисунок 2. Внешний вид образца после
окончания натурного эксперимента
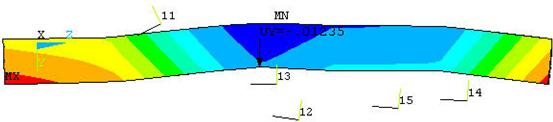
Рисунок 3. Результат расчета деформаций щита на модели
с указанием максимального прогиба
|
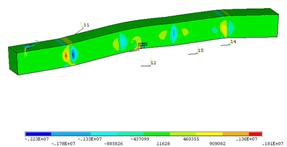
Рисунок 4. Отображение поля напряжений по толщине щита в модели |
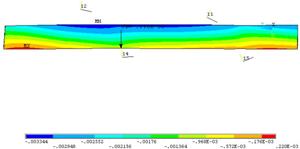
Рисунок 5. Отображение поля напряжений по ширине щита в модели |
В результате всестороннего анализа модели щита, а так же в целях уменьшения покоробленности и снижения концентрации напряжений предложена другая схема компоновки годичных слоев в смежных рейках (рис. 6). Для чего необходимо несколько реек поменять местами и перевернуть, а рейку тангенциальной распиловки заменить радиальной.
Рисунок 6. Схема компоновки годичных слоев в смежных рейках
усовершенствованной конструкции
После совершенствования конструкции столярной плиты максимальный
прогиб уменьшился в 14,5 раз и составил
|
Рисунок 7. Результат расчета деформаций щита на модели |
Рисунок 8. Изображение поля напряжений по ширине щита на
модели |
Таким образом, была найдена
оптимальная схема компоновки годичных слоев в смежных рейках столярного щита,
обеспечивающая снижение покоробленности конструкции при одновременном
уменьшении напряжений, возникающих вследствие увлажнения древесины в процессе
эксплуатации.
Проведенный анализ
конструкции показывает, что использование систем конечно-элементного анализа
позволяет выявить недостатки изделия на концептуальной стадии проекта и
исправить их до начала изготовления с учетом заданных технических условий.
Заключение.
· Предложена модель физико-механических свойств древесины при конечно-элементном анализе столярных изделий на основе цилиндрической системы координат анизотропии постоянных упругости;
· Разработана прикладная методика расчета столярных изделий, позволяющая учесть особенности анизотропии физико-механических характеристик древесного материала с учетом усушки и разбухания древесины при изменении температурно-влажностных условий окружающей среды;
· Проведено численное исследование столярного щита работающего в условиях повышенной влажности;
· Показана хорошая корреляция экспериментальных данных и результатов моделирования;
· Разработанная модель может быть применена для исследования и оптимизации столярных конструкций по условиям прочности и деформативности (например, деталей мебели и их узловых соединений), в вагоностроении (перегородки, панели, багажные полки, настил полов, встроенная мебель и другие элементы конструкций), в судостроительной промышленности (элементы конструкций полов, перегородок, дверей, стеновых панелей, встроенная мебель и другие несущие элементы конструкций), в деревянном домостроении, в производстве столярно-строительных изделий и в других отраслях народного хозяйства.
Литература.
1. Российская архитектурно-строительная энциклопедия. Т. 8: Деревянное зодчество России. – Москва: ВНИИНТПИ Госстроя России, 2002. – 325 с.
2. Зенкевич, О. Метод конечных элементов в технике / О. Зенкевич – Москва: Мир, 1975. – 541 с.
3. Уголев, Б.Н. Древесиноведение с основами лесного товароведения: Учебник для лесотехнических вузов / Б.Н. Уголев. – 3-е изд. – Москва: МГУЛ, 2002. – 340 с.
4. Древесина. Метод определения коэффициентов поперечной деформации: ГОСТ 16483.29-73*. – Введ. 01.01.1975. – Москва: Госстандарт России: ИПК Издательство стандартов, 1999. – 6 с.
5. Древесина.
Метод определения модулей сдвига: ГОСТ
16483.30-73*. – Введ. 01.01.1975. – Москва:
Госстандарт России: ИПК Издательство стандартов, 1999. – 6 с.
6. Древесина. Показатели физико-механических свойств малых чистых образцов: ГСССД 69-84. – Введ. 01.01.1985. – Москва: Госстандарт России: Издательство стандартов, 1985. – 29 с.
7. Каплун, А.Б. ANSYS в руках инженера: Практическое руководство / А.Б. Каплун, Е.М. Морозов, М.А. Олферьева. – Москва: Едиториал УРСС, 2003. – 272 с.
8. Пардаев, А.С. Принципы моделирования и анализа прочности столярных конструкций на основе метода конечных элементов / А.С. Пардаев, С.П. Трофимов // Труды БГТУ: науч. тр. / БГТУ. Сер. II. Лесная и деревообрабатывающая промышленность. – 2005. – Вып. ХIII. – С. 162–164.
Дата поступления
статьи в редакцию: 28.06.2008 г.