УДК674.023

Метод расчета режимов обработки древесины

резанием

Глебов И.Т.

ФГОУ ВПО “Уральский государственный лесотехнический университет”

В статье излагается зависимость силы резания от толщины срезаемого слоя, углов перерезания волокон древесины и расчет режимов резания

В теории резания древесины на основании экспериментальных исследований установлено, что в случае снятия лезвием срезаемого слоя толщиной а ≥ 0,1 мм, единичная касательная сила резания может быть описана уравнением (рис. 1, отрезок АВ)

, (1)

где F_х1 – единичная касательная сила резания, Н/мм; р – фиктивная сила резания, Н/мм; k – касательное давление срезаемого слоя на переднюю грань зуба, МПа; – коэффициент затупления режущей кромки лезвия; a – касательное давление, возникающее при пилении от трения стружки в пропиле, МПа; t, b – высота и ширина пропила соответственно, мм; а – толщина срезаемого слоя, мм.

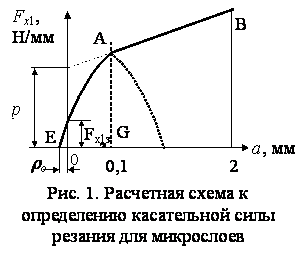
В диапазоне микрослоев (а ≤ 0,1 мм) линия зависимости единичной касательной силы резания от толщины срезаемого слоя имеет параболическую форму (рис. 1). Для упрощения расчетов в 60-х гг. прошлого столетия кривую ЕА параболы заменили прямой линией. В этом случае результаты расчетов получались заниженными по величине. В настоящее время, в условиях компьютерных технологий задача упрощения расчетов не стоит. На передний план выступает задача повышения точности расчетов.

Напишем уравнение ветви параболы ЕА. Общее уравнение параболы в осях координат F_x1 и а имеет вид

F_x1 = са² + dа + е, (2)

где с, d, е – параметры параболы.

Парабола проходит через точку Е, и вершина ее расположена в точке А.

Координаты точки А:

а_А = 0G = 0,1 = ;

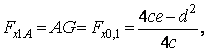
где F_{x 0,1} – значение касательной силы резания при толщине срезаемого слоя 0,1 мм: .

Отсюда получим

d = – 0,2с, 4се – d₂ = 4с F_{x 0,1}.

Точка Е, лежащая на параболе, имеет координаты:

а_Е = – r_о; F_x1Е = 0.

Подставляя эти координаты в уравнение параболы (2), получим

,

.

Получена система уравнений для определения параметров с, d, е параболы:

d = – 0,2с;

4се – d2 = 4с F_{x 0,1}; (3)

.

После решения системы уравнений получено

; ; ,

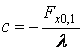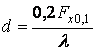где l – коэффициент: ; где r_о – начальный радиус закругления режущей кромки, мм.

Уравнение единичной касательной силы резания для микрослоев (по уравнению 2) и с учетом поправочных коэффициентов на породу а_п, влажность а_w и вид пиления а_в (встречное, попутное) имеет вид

. (4)

При решении обратных задач из уравнений для единичной касательной силы резания находят значение толщины срезаемого слоя. Сначала по величине заданной мощности определяют значение силы резания при пилении одним зубом

,

где – длина режущей кромки зуба пилы, мм.

Запишем уравнение (4) касательной силы резания для микрослоев c учетом коэффициента затупления режущей кромки зуба в виде

.

Обозначим .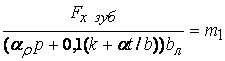

Если m₁ < 1, то расчет следует вести по формулам для микрослоев, при m₁ > 1 расчет следует вести по формулам для макрослоев.

После преобразования составим приведенное квадратное уравнение

Отсюда

. (5)

При m₁ = 1 а = 0,1 мм.

Для макрослоев толщина срезаемого слоя определяется по уравнению

. (6)

В приведенных формулах имеется два параметра (р, k), которые учитывают структуру древесины, угол перерезания волокон древесины. При резании различают три главных вида резания (торцовое, продольное, поперечное) и три промежуточных вида резания (продольно-торцовое, поперечно-торцовое, продольно-поперечное). Эти виды резания отличаются положением вектора скорости главного движения и плоскости резания относительно волокон древесины, т.е. величиной угла перерезания волокон.

При продольно-торцовом виде резания угол перерезания называют углом встречи, . При поперечно-торцовом виде резания угол перерезания называют углом наклона, . Поперечно-продольное резание характеризуют величиной угла скоса , . При продольной подаче заготовки в зависимости от положения режущих кромок инструмента относительно волокон древесины возможно резание продольно-торцовое или продольно-торцово-поперечное.

Экспериментально найденные обобщенные зависимости удельной силы резания от углов перерезания волокон для указанных видов резания по данным А.Л. Бершадского [1] приведены на рис. 2. При =0 и =0 имеет место продольное и поперечное резание соответственно. При =90° и =90° имеет место торцовое и поперечное резание соответственно. Для всех видов резания наблюдаются синусоидальные корреляционные зависимости удельной силы резания от угла перерезания волокон древесины.

Для удобства пользования экспериментальными данными кривые графиков представляют в форме уравнений. Для этого часто пользуются методом спрямления кривых. Если кривые графиков рис. 2 построить в осях координат (ось ординат) и (ось абсцисс) ординат в осях координат тодом спрямления кривых.ривые графиков надо представить в форме уравнений. но волокон древесины.), то из синусоидальных кривых получатся прямые линии типа АБ (рис. 3). Тогда, обозначив параметры F_уд и фиктивной силы резания р символом А, получим уравнения прямых линий в общем виде [2]

, , ,

(7)

Для упрощения расчетов, ориентируясь на возможности логарифмической линейки как основного средства выполнения расчетов 60-х годов прошлого столетия, А.Л. Бершадский предложил следующие формулы

, , .

(8)

Неравномерная ось абсцисс со шкалой (см. рис.3) заменена равномерной шкалой . В результате такой замены расчетные формулы дают погрешность до 14 %.

Расчетный метод А.Л. Бершадского, созданный в середине прошлого столетия, широко используется на практике в настоящее время. Пользователи практически не знают о тех допущениях и упрощениях, которые были сделаны при создании расчетного метода. В настоящее время, стремясь повысить точность расчетов, надо отказаться от указанных упрощений и расчеты значений параметров р и k выполнять по формулам (7).

На основании рекомендуемых А.Л. Бершадским расчетных формул [2] типа для определения силы резания при главных видах резания и значения эмпирических коэффициентов (таблица 1), предлагаются новые формулы для выполнения современных расчетов, которые приведены ниже.

Таблица 1

Значения эмпирических коэффициентов А, Б, В, МПа,

и р, Н/мм для древесины сосны [2]

А^	А//	А#	Б^	Б//	Б# *
0,550	0,196	0,029	0,196	0,069	0,059...0,069
В^	В//	В#	р^	р//	р#
19,62	5,40	0,59	4,80	1,57	0,98
* Меньшее значение Б# при d < 55°, большее – при d > 55°.

Расчетные формулы, рекомендуемые для определения значений параметров р и k, при переходных видах резания массивной древесины сосны:

– для продольно-торцового резания

;

;

– для поперечно-торцового резания

;

;

– для поперечно-продольного резания

;

;

– для продольно-торцово-поперечного резания

р_//-^-# = р_//–^ - (р_//–^- р_#–//);

k_//-^-# = k_//–^ - (k_//–^- k_#–//).

Здесь d подставляют в град., V'– в м/с. Кроме того,

если V £ 50 м/с, то V' = (90-V), иначе V' = V;

если d £ 55º, то С = 0,059, иначе С = 0,069.

Заключение. Устраняя допущения и упрощения, принятые основоположником расчетного метода А.Л. Бершадским в середине прошлого столетия, в статье предлагаются новые приемы определения сил резания в диапазоне микрослоев, а также расчета параметров р и k при переходных видах резания древесины. Предлагаемые формулы дополняют и развивают расчетный метод А.Л. Бершадского, повышают точность расчетов.

Библиографический список

1. Бершадский, А.Л. Резание древесины [Текст]: учеб. пособие/ А.Л. Бершадский; М.; Л. Гослесбумиздат, 1958. 328 с.

2. Бершадский, А.Л. Справочник по расчету режимов резания древесины [Текст]/ А.Л. Бершадский; М.; Гослесбумиздат, 1962. 124 с.

METHOD OF CALCULATION OF MODES LONGITUDINAL SAWing OF WOOD

Glebov I.T.

Ural state forest engineering university

In clause dependence of force of cutting on thickness of a cut off layer, corners of cutting of fibres of wood and calculation of modes of cutting is stated