УДК 628.517

В.К. Пашков, Д.Д. Шишкин

(УГЛТУ)

МЕТОДЫ И СРЕДСТВА ЭКСПЕРИМЕНТАЛЬНОЙ ОЦЕНКИ

ВИБРОАКТИВНОСТИ ГИБКИХ ВРАЩАЮЩИХСЯ ДИСКОВ

Режущие инструменты с корпусом в виде гибкого диска будут надежно работать, если положенная в основу эксплуатации форма равновесия устойчива. Для круглых плоских пил это плоская форма равновесия. Предельные значения внешних сил или факторов их обуславливающих, при которых становится возможным появление новых форм равновесия, называются критическими. При назначении рабочих частот вращения таких инструментов необходимо обеспечить их положение вне зоны динамической неустойчивости. Необходимые теоретические сведения о колебаниях и устойчивости круглых плоских пил изложены в работе [1].

Для отстройки рабочих частот пил от зон динамической неустойчивости необходимо знать, в общем случае, значения следующих параметров: статическую u_ст и динамическую u_д частоты диска; частоту назад u₁ и вперед u₂ бегущих цепей волн; число узловых диаметров l наиболее вероятной формы колебаний диска; коэффициент динамичности В; критическую частоту вращения n_кр. Эти параметры определяются экспериментально или расчетным путем.

В силу отклонений в линейных размерах, формы, начальных напряжений для одинаковых типоразмеров пил предпочтение отдают экспериментальным методам оценки виброактивности дисков. Известно несколько экспериментальных методов [2, 3, 4, 5].

На рис.1 приведена блок-схема экспериментальной установки для исследования форм l и собственных частот колебаний u_ст, u_д дисков пил.

Установка позволяет регистрировать и записывать сигнал дифференциального индуктивного датчика на осциллографе Н-008 и ЭО-7 параметров u_д (от датчика 2), u_д, u₁ и u₂ (от датчика 8) диска и число оборотов пильного вала n от датчика 9. Колебания в диске возбуждаются генератором звуковой частоты 3Г-10 при положении переключателя в позиции I. Значения частоты u_д выведены дополнительно на экран электронного частотомера (поз. II), значения n (поз. III).

Типовая осциллограмма колебаний пилы приведена на рис. 2.

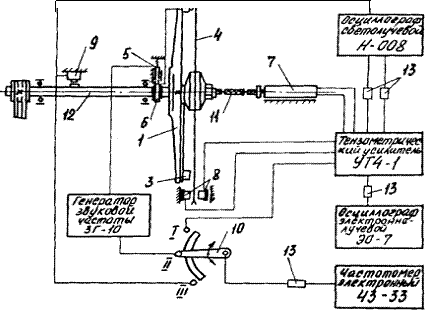
Рис. 1. Блок-схема экспериментальной установки:

1 – жесткий массивный диск; 2 – электромагнитный вибратор; 3 – индуктивный датчик; 4 – пильный диск; 5 – щетки; 6 – кольца токопроводящего устройства

к вибратору 2; 7 - ртутный токосъемник; 8 – дифференциальный индуктивный

датчик; 9 – отметчик числа оборотов; 10 – переключатель на позиции I, II и III;

11 – муфта; 12 – пильный вал; 13 – разъемы

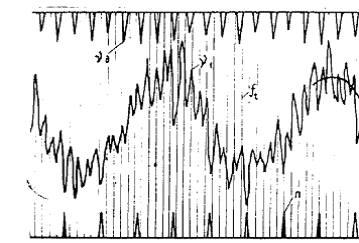
Рис. 2. Типовая

осциллограмма колебаний пильного диска по форме с двумя узловыми диаметрами

Частота записанного процесса u(u_д, u₁, u₂, n), Гц определяется из отношения

u = (f_t K) / K_t, (1)

где f_t – частота отметчика времени, f_t = 100 Гц;

K_t – число отметок времени;

К – число периодов записанного процесса на длине осциллограммы,

соответствующей значению K_t.

Определим параметры колебательного процесса пильного диска (рис. 2) по формуле (1): частота вращения пилы n = 100/41 = 19,5 с^-1; частота вперед бегущей волны колебаний по диску u₁ = 100/21 = 85,7 Гц; назад бегущей волны u₂ = 100∙1/21 = 4,9 Гц; динамическая частота u_д = 100/8/17 = 47 Гц.

Статическая частота u_ст определяется по экрану электронного частотомера Ч3-33 визуально при n = 0, а форма колебаний – по количеству всплесков амплитуды колебаний на экране осциллографа при повороте вала вручную на один оборот. Только после этого вал разгоняется до заданного числа оборотов. Частота диска в статике u_ст = 31,2 Гц. Остальные параметры колебательного процесса пилы определяются расчетом.

Динамический коэффициент В определяется по формуле

В = (u_д² - u_ст²)/n² ; (2)

В = (47² – 31,2²)/19,5² = 3,2.

Число узловых диаметров (форма колебаний) l определяется по формуле

l = (u₁ - u₂ )/2n ; (3)

l = (85,7 - 4,8)/(2 ∙19,5) = 2.

Критическая частота вращения n_кр определяется по формуле

n_кр = u_д/l ; (4)

n_кр = 47/2 =23,5 с^-1.

Рабочая частота вращения пилы должна удовлетворять неравенству

n_раб 0,85 n_кр . (5)

В нашем случае n_раб = 19,5 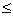0,85∙23,5 = 20 с^-1.

Описанный метод точен, но при этом требуется сложная экспериментальная установка и неприемлем для исследования колебаний дисков при резании. В этом случае используют два неподвижных датчика колебаний, размещенных на одной окружности с центральным углом j, например 30⁰. Датчиками регистрируются параметры u₁, u₂. Форму колебаний устанавливают по сдвигу фаз между кривыми, записанными разными датчиками по назад бегущим волнам i. Если этот сдвиг выразить в долях периода рассматриваемой длины волны, то число узловых диаметров l будет равно

l = 360 / (q i). (6)

Резонансные колебания в пиле поддерживаются двумя электромагнитными вибраторами, один из которых работает с частотой u₁, второй с частотой u₂. Схема размещения дифференциальных индуктивных датчиков и вибраторов приведена на рис. 3,а. Установка отличается от описанной

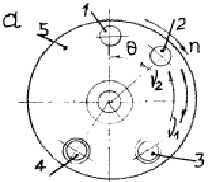
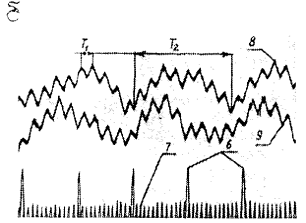
Рис. 3. Схема регистрации колебательного процесса диска пилы:

а – размещение датчиков и вибраторов относительно диска; б – осциллограмма колебаний диска с λ = 2; 1, 2 – дифференциальные индуктивные датчики;

3, 4 – электромагнитные вибраторы; 5 – пила; 6 – отметки оборотов пилы n;

7 – отметчик времени f_t (f_t = 500 Гц); 8, 9 – колебания диска пилы, записанные

соответственно датчиками 1 и 2; Т₁, Т₂ – периоды полного колебания

соответственно для вперед u₁ и назад u₂ бегущих волн

выше отсутствием жесткого диска с вибратором и датчиком, установленными на нем.

На рис. 3,б приведена типовая осциллограмма колебаний диска пилы с l = 2. Записи на осциллограммах соответствуют нарастанию времени слева направо.

Определим по осциллограмме (см. рис. 3,б) параметры u₁, u₂, l, u_д с учетом формул (1)-( 5). На четырех оборотах пилы размещается 51 отметка времени f_t, следовательно, пила вращается со скоростью n =/51 = 39,2 с^-1. В интервале семи оборотов укладывается четыре волны с низкой частотой u₂ и 32 волны с высокой частотой u₁, тогда u₂ = = 22,4 Гц, а u₁ = = 179,2 Гц.

Цепь волн с низкой частотой достигает датчика 2 раньше, чем датчика 1. Сдвиг по фазе составляет 1/6 расстояния между двумя максимальными амплитудами верхней и нижней кривой. Это свидетельствует, что зарегистрирована назад бегущая цепь волн, центральный угол между соседними максимальными амплитудами составляет 30 = 180⁰, а диск совершает колебания с λ = 2. Действительно, по формуле (3) l = (179,2 – 22,4)/(2) = 2 .

Динамическую частоту u_д определяем по формуле

u_д = u₁ - 2 n ; (7)

u_д = 179,2 – 2 = 100,8 Гц.

В неподвижном диске при возбуждении в нем колебаний датчики регистрируют одну и ту же частоту собственных колебаний u_ст = 82,5 Гц.

Динамический коэффициент определяем по формуле (2)

В = (100,8² – 82,5²)/39,2² = 2,19. Критическая частота вращения по (4)

n_кр = 100,8/2 = 50,4 с^-1.

Параметры колебаний пилы, в случае необходимости, можно определить по частоте лишь одной из бегущих волн. Для этого достаточно записать процесс колебаний с узловыми диаметрами l для трех различных произвольных частот вращения n₁, n₂ и n₃ [4]. При их определении по вперед бегущей цепи волн u₁ составляется система уравнений:

(u₁₁ - ln₁ )² = u_ст² + Bn₁² ;

(u₁₂ - ln₂ )² = u_ст² + Bn₂² ; (8)

(u₁₃ - ln₃ )² = u_ст² + Bn₃² .

Значения В и u_ст определяются решением совместно любой пары уравнений (8):

В = [(u₁₂ - ln₂ )² - (u₁₁ - ln₁ )²] / (n₂² - n₁²) ;

u_ст = {((u₁₁ - ln₁ )² n₂² - (u₁₂ - ln₂ )² n₁²)/(n₂² - n₁²)}^0,5. (9)

Число узловых диаметров l находим, подставляя в неиспользованное уравнение системы (8), выражений В и u_ст из формулы (9)

l = 0,5 [u₁₁( n₃² - n₂²) - u₁₂( n₃² - n₁²) + u₁₃( n₂² - n₁²)]/

[u₁₁n₁( n₃² - n₂²) - u₁₂n₂( n₃² - n₁²) + u₁₃n₃ ( n₂² - n₁²)] . (10)

Аналогично составляются уравнения для случая определения параметров колебаний пилы по назад бегущей цепи волн.

В работе [5] авторами предложен метод, который позволяет задать форму колебаний l в начале эксперимента специальной расстановкой акустических вибраторов и устранить трудоемкую операцию их расчета. Блок-схема установки с регулируемой частотой вращения приведена на рис.4.

Вибраторы устанавливают неподвижно с одной стороны пилы против ее периферийной зоны. При колебаниях пилы с l = 2 центральный угол между вибраторами q = 90⁰; для l = 3 q = 60⁰; для l = 4 q = 45⁰. Питание среднего вибратора осуществляется от генератора в противофазе с питанием двух других вибраторов. Колебания пилы воспринимает датчик колебаний, сигнал которого поступает на осциллограф и цифровой частотомер. Синхронизация развертки изображения на экране осциллографа с частотой вращения пилы осуществляется с помощью датчика одного оборота.

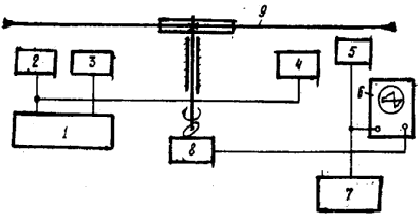
Рис. 4. Блок схема экспериментальной установки:

1– звуковой генератор 3Г-10; 2,3, 4 – акустические вибраторы; 5 – датчик

колебаний; 6 – осциллограф С9-4; 7 – цифровой электронный

частотомер Ч3-34; 8 – датчик одного оборота; 9 – пила

Типовые осциллограммы колебаний пилы для n = 13 с^-1, λ = 2 приведены на рис. 5.

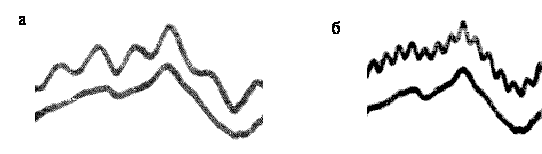
Рис. 5. Осциллограммы колебаний:

а – резонансной назад бегущей цепи волн за время одного оборота;

б – то же вперед бегущей (нижняя кривая – развертка профиля диска)

Момент резонанса устанавливается по максимуму амплитуды колебаний u₁ и u₂, а их измерение выполняется с помощью частотомера. Для условий, соответствующих рис. 5, u = К n, где К – число экстремумов одного знака на осциллограммах за время одного оборота; u₂ = 8 = 78 Гц;

u₁ = 16= 182 Гц. Рассчитываем: динамическую частоту по формуле u_д = u₂ + l n; В по формуле (2); n_кр по формуле (4).

Выбор метода и средств экспериментальной оценки вибрационной активности вращающихся гибких дисков требует учета условий, при которых будет выполняться оценка, ее целей, требуемой точности измерений.

ЛИТЕРАТУРА

1. Пашков В.К. Колебания и устойчивость дереворежущих круглых пил : В кн. Вибрация. Шум. Вибродиагностика : Матер. межгос. науч.-техн. семинара «Виброакустические процессы в технологиях, оборудовании и сооружениях лесопромышленного комплекса», 23-25 ноября 1999 г. / Урал. гос. лесотехн. акад. -Екатеринбург, 2000. – С. 56-63.

2. Кэмпбелл В. Аксиальная вибрация дисков паровых турбин и меры защиты от нее. – М.-Л.: ОНТИ, 1987. – 136 с.

3. Левин А.В. Рабочие лопатки и диски паровых турбин. – М.: Госэнергоиздат, 1953. – 624 с.

4. Об экспериментальных методах определения критических оборотов тонких дисков / В.К. Пашков, В.Г. Бодалев, Э.М. Туриков, А.И. Шевченко // Изв. ВУЗ. Лесной журнал. – 1973. – № 6. – С. 63-68.

5. Дунаева В.В., Дунаев В.Ф. Экспериментальный метод исследования колебаний дисковых пил // Изв. ВУЗ. Лесной журнал. – 1982. – № 2. –С. 99-103.

METHODS AND MEANS OF EXPERIMENTAL ESTIMATION ВИБРОАКТИВНОСТИ OF FLEXIBLE ROTATING DISKS