Глебов И.Т., Кузнецов А.И. (УГЛТУ, г. Екатеринбург, РФ) GIT5@yandex.ru
Исследование состояния точности
деревообрабатывающих станков в учебном
процессе
Технологическая точность
деревообрабатывающего станка характеризуется фактическими погрешностями
размеров и формы, обработанных на станке деталей в сравнении с размерами и формой, заданными на чертеже.
Получаемые на станке размеры деталей зависят от многих факторов, таких как:
– геометрических погрешностей станка,
инструмента, приспособлений;
– погрешностей настройки;
– жесткости упругой технической
системы "станок";
– неоднородности свойств древесины;
– нестабильности режима обработки;
– человеческого фактора: умений,
навыков, утомленности станочника, его психологического состояния;
– состояния окружающей среды и др.
Все эти факторы действуют
одновременно, зависят друг от друга и формируют конечный размер детали,
обрабатываемой на станке. В связи с этим процесс размерообразования при анализе
рассматривается системно. Процесс образования на станке размеров и формы
деталей соответствует состоянию технологической системы. Эта система динамичная, постоянно меняющая
свое состояние во времени. Образующиеся размеры деталей носят случайный
характер, поэтому систему называют еще вероятностной. Для исследования таких
систем используют методы теории вероятности и математической статистики.
Математические методы позволяют по
параметрам небольшой выборки с заданной точностью судить о параметрах
генеральной совокупности. Они позволяют определить тенденцию изменения точности
обработки деталей на станке и установить момент, когда фактический размер
детали может выйти за пределы поля допуска. Знание этого момента времени дает
возможность управлять процессом обработки деталей.
Изучение на лабораторных работах математических
методов в приложении к управлению точностью процесса обработки деталей
позволяет улучшить качество продукции. Обучающиеся имеют возможность научиться,
получить умения и навыки по исследованию точности станков, точности настройки
станков на размер.
Определение точности станка. В лабораторной работе по учебной дисциплине “Оборудование
отрасли” исследуется точность рейсмусового станка. Точность станка
регламентирована нормами точности по ГОСТ 7228-75 и задана допуском величиной
Точность станка определяется путем исследования
выборки, взятой из генеральной совокупности при обработке партии деталей. Для
образования выборки обследуют не менее 50 обработанных деталей. При этом
контролируемый размер измеряют в трех местах детали длинной 1000 мм: посередине
и в
Далее находят центр группирования
размеров партии деталей (среднее арифметическое значение):
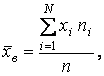
где хi - среднее значение интервала;
ni - частота (число размеров деталей в
интервале);
n - количество измерений размеров в
совокупности.
Находят среднее квадратичное
отклонение выборки по формуле:
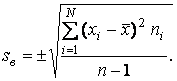
Поле рассеяния размеров партии
деталей, обработанных на станке, может быть найдено по формуле:
w = 6sв.
С учетом погрешности на размерную
настройку станка допуск квалитета будет:
ITq = 6,6 sв.
Пример обработки выборки при
определении точности размеров деталей, обработанных на станке, приведен в табл.
1.
Таблица 1
Пример протокола статистической обработки
результатов измерений
|
№ интервалов |
Границы интервалов, мм |
Середина интервала xi, мм |
Частота ni, т. |
xi ni |
xi- |
(xi- |
(xi- |
|
1 |
31,80-31,84 |
31,82 |
6 |
190,92 |
-0,1866 |
0,0348 |
0,2091 |
|
2 |
31,85-31,88 |
31,86 |
7 |
223,02 |
-0,1466 |
0,0215 |
0,1506 |
|
3 |
31,89-31,92 |
31,90 |
9 |
287,1 |
-0,1066 |
0,0114 |
0,1024 |
|
4 |
31,93-31,96 |
31,94 |
15 |
479,1 |
-0,0666 |
0,0044 |
0,0667 |
|
5 |
31,97-32,00 |
31,98 |
27 |
863,46 |
-0,0266 |
0,0007 |
0,0192 |
|
6 |
32,01-32,04 |
32,02 |
35 |
1120,7 |
0,0133 |
0,0002 |
0,0062 |
|
7 |
32,05-32,08 |
32,06 |
28 |
897,68 |
0,0533 |
0,0028 |
0,0796 |
|
8 |
32,09-32,12 |
32,10 |
10 |
321,0 |
0,0933 |
0,0087 |
0,0871 |
|
9 |
32,13-32,16 |
32,14 |
8 |
257,12 |
0,1333 |
0,0178 |
0,1422 |
|
10 |
32,17-32,20 |
32,18 |
5 |
160,9 |
0,1733 |
0,0300 |
0,1502 |
|
Итого: |
150 |
4801 |
|
|
1,0133 |
||
Величина интервала ![]() =
=![]() 0,04 мм.
0,04 мм.
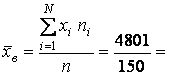 32,0 мм.
32,0 мм.
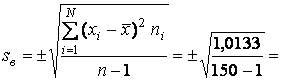 0,082 мм.
0,082 мм.
ITq = 6,6×sв = 6,6×0,082= 0,5442 мм
По ГОСТ 6449.1-82 находим, что для
размера
Определение настроенности
рейсмусового станка. Пусть случайная величина толщины столярных
щитов Х, обрабатываемых на рейсмусовом станке, имеет нормальное
распределение. Выборка объемом n = 50,
извлеченная из генеральной совокупности, имеет следующее распределение частот:
|
хi, мм |
15,5 |
15,7 |
16,9 |
16,1 |
|
ni |
10 |
18 |
12 |
10 |
Точность станка, определяемая среднеквадратическим
отклонением, задана и равна sо = 0,3 мм.
Определить настроенность станка при обработке щитов по
толщине, если толщина деталей по чертежу равна 16Is14 (16±0,215 мм).
Настроенность станка определяют по центру настройки
![]() , равному математическому ожиданию
[1]. Возможны оценки в виде точечного значения
, равному математическому ожиданию
[1]. Возможны оценки в виде точечного значения ![]() или в виде интервала,
который с известной степенью доверия (доверительной вероятностью) включает
неизвестное значение m.
или в виде интервала,
который с известной степенью доверия (доверительной вероятностью) включает
неизвестное значение m.
Интервал может быть:
- двусторонним, если необходима уверенность с
заданной доверительной вероятностью, в каких пределах может лежать m;
- односторонним с верхней границей, если необходима
уверенность, что m не выше какого-то значения;
- односторонним с нижней границей, если необходима
уверенность, что m не ниже
какого-то значения.
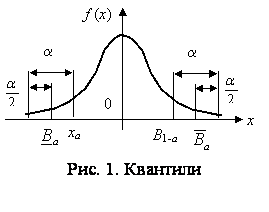 Для решения задачи используют квантили (рис. 1). Квантилем
уравнения a (a квантиль)
называется такое значение хa случайной
величины Х, при котором ее функция распределения принимает значение, равное a. Для непрерывной случайной величины квантили – это
такие границы, которые делят всю вероятность на четыре равные части. Различают
три квантили: левую (Q1=1/4), центральную (Q2=1/2) и правую (Q3=1/4).
Для решения задачи используют квантили (рис. 1). Квантилем
уравнения a (a квантиль)
называется такое значение хa случайной
величины Х, при котором ее функция распределения принимает значение, равное a. Для непрерывной случайной величины квантили – это
такие границы, которые делят всю вероятность на четыре равные части. Различают
три квантили: левую (Q1=1/4), центральную (Q2=1/2) и правую (Q3=1/4).
Решение. Принимаем доверительную вероятность
(надежность) оценки (уровень значимости) 1 - a = 0,95.
1. Квантиль стандартного
нормального закона распределения уровня (1 - a) по таблице значений функций
стандартного нормального закона распределения:
U1-a = Ф(1,5+z)= 1,5+0,14 =1,64.
2. Квантиль стандартного
нормального закона распределения уровня (1 - a/2). Если 1 - a = 0,95, то a = 0,05, a/2 = 0,025, 1 - a/2 = 0,975 и квантиль уровня (1 - a/2) по таблице значений функции:
U1-a/2 = 1,5+ 0,46 =1,96.
3. Находим общую выборочную среднюю:
![]() мм.
мм.
4. Вычисляем коэффициенты
![]() мм,
мм,
![]() мм.
мм.
5. Результаты оценки настроенности
станка.
5.1. Точечная оценка параметра
m: ![]() = 16,008 мм.
= 16,008 мм.
5.2. Двусторонний
симметричный доверительный интервал для m:
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
5.3. Односторонние
доверительные интервалы для m:
![]() ,
, ![]() ,
,
![]() или
или ![]() .
.
![]() или
или ![]() .
.
Вывод. Сравнивая заданный
размер детали 16±0,215 мм (16,215…15,785)
мм с границами расчетных доверительных интервалов m, убеждаемся, что размеры
толщины деталей укладываются в пределах поля допуска. Станок настроен
правильно.
Проверка правильности настройки
станка на настроечный размер при известной точности. Пусть на деревообрабатывающем станке обрабатывается деталь с одним из
размеров 15-
![]() ,
,
где d – номинальный размер, мм;
ei – нижнее предельное отклонение
размера, мм;
mо – заданное значение размера, мм.
![]() =
=
Из генеральной совокупности извлечена выборка
размеров обработанных деталей объемом n = 30.
Распределение частот выборки:
|
хi |
14,82 |
14,84 |
14,86 |
14,88 |
14,90 |
|
ni |
3 |
6 |
10 |
7 |
4 |
Сравнить неизвестное среднее
значение с заданным значением mо при
известной дисперсии D = s2, и доказать, что
математическое ожидание всей генеральной совокупности будет не меньше
настроечного размера.
Решение. 1. Принимаем значение уровня
значимости a = 0,01 и определяем доверительную
вероятность (надежность) оценки р = 1 - a = 0,99. При уровне значимости a/2 = 0,005 доверительная вероятность р
= (1 - a/2) = 0,995.
2. По таблице значений
функции стандартного нормального закона распределения принимается квантиль уровней (1 - a) и (1 - a/2).
Значение квантили U(1-a) уровня (1 - a) находят
как значение аргумента U, соответствующего
значению функции Ф(u) = 1-a:
U(1-a)= 2,0+0,33= 2,33;
U(1-a/2)= 2,5+0,08= 2,58.
3. Находим среднее выборочное
значение
![]() 14,862 мм.
14,862 мм.
Результаты
Сравнение выборочного
среднего значения ![]() с заданным значением mо:
с заданным значением mо:
1. В двустороннем случае:
предположение равенства выборочного среднего и заданного значений (нулевая
гипотеза) отклоняется, если ![]() ;
;
![]() ;
; ![]() ,
,
таким образом,
предположение равенства ![]() и m0 отклоняется.
и m0 отклоняется.
2 В одностороннем случае:
– предположение о том,
что выборочное среднее не менее чем m0 (нулевая
гипотеза) отклоняется, если
![]() ;
; ![]()
14,862<14,79, не
отклоняется;
– предположение о том,
что выборочное среднее не более чем m0 (нулевая гипотеза) отклоняется, если
![]() ;
; ![]()
14,862>14,79,
отклоняется.
Таким образом, на
основании выборки доказано, что математическое ожидание генеральной
совокупности контролируемого размера не меньше настроечного размера.
Библиографический список
1. Глебов, И.Т.
Технологическая точность деревообрабатывающих станков[Текст] И.Т. Глебов, А.Ю.
Вдовин/ Екатеринбург, УГЛТУ, 2006. 135 с.
RESEARCH OF THE
CONDITION OF ACCURACY ДЕРЕВООБРАБАТЫВАЮЩИХ OF MACHINE TOOLS IN EDUCATIONAL PROCESS