ОПТИМИЗАЦИЯ СТРУКТУРЫ И ВЕЛИЧИНЫ ПАРАМЕТРОВ РЕЖИМОВ КОНВЕКТИВНОЙ СУШКИ ПИЛОМАТЕРИАЛОВ

А.Г. Гороховский, Е.Е. Шишкина, А.А. Гороховский

(УГЛТУ, г. Екатеринбург, РФ) elenashishkina@yandex.ru

The optimization of structure and value parameters ways convection drying lumber.

Рассмотрены вопросы, касающиеся влияния режима сушки на качество высушенной древесины. Проведена оптимизация режимов сушки по требуемой категории качества.

Анализируя мнение основоположников отечественной науки о сушке древесины Н.С. Селюгина [1], П.С. Серговского [2] и И.В. Кречетова [3] можно выделить следующие основные факторы, определяющие качество сушки пиломатериалов:

· требования к качеству сушки

· контроль качества

· свойства древесины, как материала, подвергаемого сушке

· технология сушки

РТМ [4] нормируют требования к качеству сушки, устанавливая при этом:

· категории качества сушки

· перечень показателей качества сушки, к которым относятся:

а) Соответствие средней влажности высушенных пиломатериалов в штабеле заданной конечной влажности;

б) Величина отклонений влажности отдельных досок или заготовок от средней влажности пиломатериалов в штабеле;

в) Перепад влажности по толщине пиломатериалов (заготовок);

г) Остаточные напряжения в высушенных пиломатериалах (заготовках).

· Значение показателей и условия их определения.

Показатели качества сушки пиломатериалов (заготовок) подлежат нормированию. Нормы устанавливаются в зависимости от категории качества сушки и условий эксплуатации изделий [4].

Вопросы, касающиеся влияния режимов сушки на качество сушки пиломатериалов, весьма подробно исследованы в 50-е – 80-е годы [2, 5 – 9 и др].

П.С. Серговский, один из основоположников отечественной науки о сушке древесины, в [2, 5, 6] отмечает, что от режима сушки зависят не все качественные показатели, а только два из них: целостность материала, обусловленная величиной полных внутренних напряжений в древесине, и степень сохранения прочности древесины, обусловленная уровнем и длительностью температурных воздействий на нее.

Построение режимов сушки должно производиться таким образом, что по ходу всего процесса максимальные значения внутренних напряжений в древесине не превысили максимально допустимой величины. Режим характеризуется коэффициентом безопасности:

, (1)

где σ_пр.р. – расчетный предел прочности древесины;

σ_макс – максимальная величина внутренних напряжений.

Оптимальным является (по мнению авторов) такая величина параметров сушильного агента (t и φ), при которой В = 1. Если В < 1, то режим не обеспечивает сохранения целостности материала, если В > 1, не достигается максимально возможная интенсивность процесса. При этом сам П.С. Серговский не дает ответа на вопрос о возможных (допустимых) отклонениях величины Б при разработке и практическом изменении конкретного режима, а Л.П. Красухина [8] дает величину ± 0,02, т.е. ± 2 %. Однако РТМ [10] для предела прочности древесины дает значение коэффициента вариации 10 %. При этом качество сушки может быть полностью гарантировано при В = 1,3 (с вероятностью р = 99, 87 %) [11]. Соответственно, при В = 1,2 гарантировано с вероятностью р = 95 %, а при В = 1,1, р = 90 %.

Совокупность параметров режима однозначно определяет величину показателей эффективности и качества высушиваемой древесины [11]. Следовательно, задача о повышении значений данных показателей может рассматриваться как оптимизационная (рис. 1).

Рис. 1. Постановка задачи оптимизации процесса сушки древесины

Х – вектор управляющих факторов;

У1 – вектор параметров эффективности;

У2 – вектор параметров качества.

Для математического описания процесса низкотемпературной конвективной сушки неограниченной пластины (пиломатериала) А.В. Лыков [12, 13], М.С. Смирнов [14] и Г.С. Шубин [15] предлагают следующую систему дифференциальных уравнений в частных производных (ДУЧП).

, (2)

, (3)

Для неограниченной пластины начальные и граничные условия III рода имеют вид:

, (4)

, (5)

(6)

(7)

Условие симметрии:

(8)

где t – температура, ⁰С;

u – влажность;

τ – время, с;

а – коэффициент температуропроводности, м²/с;

а_m – коэффициент влагопроводности, м²/с;

ε – коэффициент фазового превращения;

ρ – плотность древесины, кг/м³;

с – теплоемкость древесины, кДж/(кг·град);

δ – термоградиентный коэффициент;

х – координата в направлении толщины пластины, м;

R – половина толщины пластины, м;

λ – коэффициент теплопроводности, Вт/(м·град);

α – коэффициент теплообмена, Вт/(м²·град);

α_m – коэффициент влагообмена, м/с;

ρ_б – базисная плотность древесины, кг/м³;

t_с – температура среды, ⁰С;

u_р – равновесная влажность древесины.

Для решения системы (2) – (8) разработано программное обеспечение (ПО) в вычислительной среде Mathcad – 14 [16] на основе неявного метода [17, 18, 19]. Кроме того, использовалось ПО для расчета внутренних напряжений [11] на основе многостержневой модели доски [20]. Используя вышеупомянутое ПО был реализован вычислительный эксперимент. Постоянными факторами при проведении эксперимента были следующие:

1.Вид пиломатериала – условный (сосна, сечение 40х150 мм);

2.Тип режима – бесступенчатый [11]

- температура обрабатывающей среды

; (9)

- равновесная влажность

, (10)

где t_н, t_к – соответственно, начальная и конечная температура агента сушки, ⁰С;

u_н, u – соответственно, начальная и текущая влажность древесины;

u_рн, u_рк – соответственно, начальное и конечное значение равновесной влажности;

b₀, b₁ – коэффициенты.

Выражение (10) представляет собой функцию желательности [21], которая характеризуется двумя переходными значениями u, обозначенными соответственно u_п1 и u_п2. Причем u_п2 = 0,35 и u_н = 0,6 – оставались постоянными во всех опытах. Теплофизические характеристики древесины и среды определялись по известным выражениям Г.С. Шубина [15]. Переменные факторы при проведении эксперимента: u_рн (х1), u_рк (х2), u_п1 (х3), t_н (х4), t_к (х5).

Факторы варьировались на трех уровнях, их значения в кодированном и натуральном выражении представлены в табл. 1.

Выходные параметры:

τ1 (у1) – продолжительность сушки пиломатериалов до влажности W = 12 %;

τ2 (у2) – продолжительность сушки пиломатериалов до влажности W = 7 %;

S_т (у3) – перепад влажности по толщине доски [4];

S_w (у4) – среднеквадратическое отклонение влажности [22, 23];

B_min (у5) – минимальное значение критерия безопасности режима в процессе каждой сушки.

Таблица 1

Переменные факторы при проведении вычислительного эксперимента

№ п/п	Факторы	Значение фактора на уровнях
		Нижний			Основной				Верхний
		Кодир.		Натур.	Кодир.		Натур.		Кодир.		Натур.
1	uрн (х1)	-	0,1			0		0,14		+		0,18
2	uрк (х2)	-	0,02			0		0,03		+		0,04
3	uп1 (х3)	-	0,1			0		0,15		+		0,2
4	tн (х4)	-	60			0		70		+		80
5	tк (х5)	-	80			0		90		+		100

В процессе эксперимента был реализован план Хартли [24], состоящий из 27 опытов. В результате были получены зависимости каждого выходного параметра от входных в виде полиномов второго порядка.

Затем проводилась оптимизация по каждому из выходных параметров (τ1, τ2, S_т, S_w, B_min).

Постановка задач оптимизации была следующая:

(11)

(12)

(13)

(14)

(15)

где

Результаты оптимизации, проведенной в вычислительной системе Mathcad-14 (с применением процедуры Given-Minimize) приведены в табл. 2.

Однако наибольший интерес представляют результаты оптимизации режима по требуемой категории качества (табл. 3). Постановка задачи оптимизации была следующей:

I категория качества:

(16)

II категория качества:

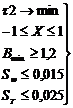(17)

III категория качества:

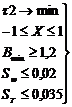(18)

Таблица 2

Результаты оптимизации режима сушки по частным критериям

№ п/п	Управляющий фактор	Значения управляющих факторов для критериев оптимальности
		τ1 (час)	τ2 (час)	ST	Sw	Bmin
1 2 3 4 5	uрн uрк uп1 tн, ^0С tк, ^0С	0,1 0,02 0,2 80 92	0,1 0,02 0,174 80 100	0,18 0,04 0,1 60 100	0,18 0,04 0,1 60,5 99,5	0,18 0,02 0,1 80 100
Значение критерия оптимальности		90,8	120	0,011	0,088	2,039

Таблица 3

Результаты оптимизации режимов сушки по категориям качества

№ п/п	Управляющий фактор / критерий качества	Значения управляющих факторов / критериев оптимальности
		I	II	III
1	uрн	0,168	0,11	0,1
2	uрк	0,036	0,033	0,038
3	uп1	0,1	0,1	0,2
4	tн, ^0С	66,25	74,7	80
5	tк, ^0С	100	100	100
6	τ2 (час)	247	179	143
7	Bmin	1,703	1,299	1,263
8	ST	0,019	0,03	0,035
9	Sw	0,01	0,015	0,02

На основании проведенных исследований можно сделать следующие выводы:

1. Режим сушки определяет все качественные показатели сушки древесины.

2. Целесообразно выбирать режим сушки, исходя из требуемой категории качества сушки, хотя действующие РТМ [4] это не предусматривают.

3. Выбор режима соответственно категории качества позволяет существенно снизить продолжительность сушки, а значит и расход энергии. Кроме того, это позволит иметь большую производительность камеры.

4. Высокое качество сушки (даже соответствующее I категории) может быть достигнуто без применения влаготепло- и кондиционирующей обработки пиломатериалов.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Селюгин, Н.С. Сушка древесины [Текст] / Н.С. Селюгин. М.; Л.: Гослестехиздат, 1949.

2. Серговский, П.С. Гидротермическая обработка древесины [Текст] / П.С. Серговский. М.: Лесн. пром-сть, 1975.

3. Кречетов, И.В. Сушка древесины [Текст] / И.В. Кречетов. М.: Лесн. пром-сть, 1977.

4. Руководящие технические материалы по технологии камерной сушки древесины [Текст]. Архангельск: ЦНИИМОД, 1985.

5. Серговский, П.С. О рациональных режимах сушки пиломатериалов в воздушных камерах периодического действия [Текст] / П.С. Серговский // Деревообрабатывающая промышленность. 1969. № 2. С. 1 – 4.; № 3. С.1 – 4.

6. Серговский, П.С. О рациональных режимах сушки пиломатериалов в высокотемпературных сушилках [Текст] / П.С. Серговский // Деревообрабатывающая промышленность. 1962. № 1. С. 4 – 8.; № 2. С. 2 - 6.

7. Николайчук, М.В. Оптимальная степень насыщенности сушильного агента в процессе сушки пиломатериалов хвойных пород при пониженных температурах [Текст] / М.В. Николайчук // Механическая обработка древесины. 1973. № 1.

8. Красухина, Л.П. О рациональных режимах сушки березовых пиломатериалов в камерах периодического действия [Текст] / Л.П. Красухина // Деревообрабатывающая промышленность. 1988. № 6. С. 5 - 7.

9. Серговский, П.С. Новые режимы сушки осиновых пиломатериалов [Текст] / П.С. Серговский, А.А. Фахретдинов // Деревообрабатывающая промышленность. 1991. № 1. С. 4 - 7.

10. Руководящие технические материалы: Древесина. Показатели физико-механических свойств [Текст]. М.: Стандартгиз, 1962.

11. Гороховский, А.Г. Технология сушки пиломатериалов на основе моделирования и оптимизации процессов тепломассопереноса в древесине [Текст]: дисс. … д-ра техн. наук / Гороховский Александр Григорьевич. СПб, 2008.

12. Лыков, А.В. О предельных переходах системы дифференциальных уравнений тепломассопереноса [Текст] / А.В. Лыков // Инженерно-физический журнал. 1973. Т. XXIV. № 1. С. 152 - 155.

13. Лыков, А.В. О системах дифференциальных уравнений тепломассопереноса в капиллярно-пористых телах [Текст] / А.В. Лыков // Инженерно-физический журнал. 1974. Т. ХХVI. № 1. С. 18 - 25.

14. Смирнов, М.С. О системе дифференциальных уравнений процесса сушки [Текст] / М.С. Смирнов // Инженерно-физический журнал. Т. IV. № 9. С. 40 - 44.

15. Шубин, Г.С. Сушка и тепловая обработка древесины [Текст] / Г.С Шубин. М.: Лесн. пром-сть, 1990. 336 с.

16. Кирьянов, Д.В. Mathcad – 12 [Текст] / Д.В. Кирьянов. СПб.: БХВ – Петербург, 2005.

17. Гаврилова, Р.И. Исследование процесса сушки с переменными коэффициентами тепло- и массопереноса [Текст] / Р.И. Гаврилова // Инженерно-физический журнал. Т. VII. № 8. 1964. С. 37 - 42.

18. Логинов, Л.И. Численное интегрирование системы уравнений тепломассообмена с помощью неявных формул [Текст] / Л.И. Логинов, П.П. Юшков // Инженерно-физический журнал. Т. III. № 10. 1960. С. 93 - 108.

19. Юшков, П.П. О численном интегрировании уравнения теплопроводности в случае, когда термические коэффициенты зависят от температуры [Текст] / П.П. Юшков // Инженерно-физический журнал. Т. I. № 9. 1958. С. 102 - 108.

20. Уголев, Б.Н. Контроль напряжений при сушке древесины [Текст] / Б.Н. Уголев, Ю.Г. Лапшин, Е.В. Кротов. М.: Лесн. пром-сть. 1980. 206 с.

21. Пижурин, А. А. Основы моделирования и оптимизации процессов деревообработки [Текст] / А. А. Пижурин, М. С. Розенблит / М.: Лесная промышленность, 1988.

22. Пинчевская, Е.А. Прогнозирование уровня качества сушки пиломатериалов [Текст] / Е.А. Пинчевская // Деревообрабатывающая промышленность. 2008. № 3. С. 8 - 12.

23. Пинчевская, Е.А. Оценка качества сушки пиломатериалов с учетом изменчивости свойств материала и среды [Текст] / Е.А. Пинчевская // Деревообрабатывающая промышленность. 2008. № 4. С. 9 - 12.

24. Пен, Р.З. Статистические моделирования и оптимизации процессов ЦБП [Текст] / Р.З. Пен / Красноярск: Изд-во Красноярского ун-та. 1982.